Advertisements
Advertisements
Question
From a point in the interior of an equilateral triangle, perpendiculars are drawn on the three sides. The lengths of the perpendiculars are 14 cm, 10 cm and 6 cm. Find the area of the triangle.
Solution
Let ABC be an equilateral triangle and O be the interior point and AQ, BR and CP are the perpendiculars drawn from point O such that OQ = 10 cm, OR = 6 cm, OP = 14 cm.
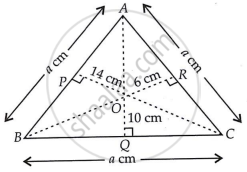
Let sides of an equilateral triangle be a cm.
Area of ΔOAB = `1/2 xx AB xx OP`
= `(1/2 xx a xx 14)cm^2`
= 7a cm2 ...(i)
Area of ΔOBC = `1/2 xx BC xx OQ`
= `(1/2 xx a xx 10)cm^2`
= 5a cm2 ...(ii)
Area of ΔOAC = `1/2 xx AC xx OR`
`(1/2 xx a xx 6)cm^2`
= 3a cm2 ...(iii)
∴ Area of ΔABC = Area of (ΔOAB + ΔOBC + ΔOAC)
= (7a + 5a + 3a) cm2
= 15a cm2 ...(iv) [From (i), (ii) and (iii)]
Area of an equilateral ΔABC = `sqrt(3)/4 a^2` ...(v)
From (iv) and (v),
`sqrt(3)/4 a^2 = 15a`
`\implies a = (60sqrt(3))/3 = 20sqrt(3)`
Substituting `a = 20sqrt(3)` in (v), we get
Area of ΔABC = `sqrt(3)/4 (20sqrt(3))^2`
= `300sqrt(3)`
Thus, the area of an equilateral triangle is `300sqrt(3) cm^2`.
APPEARS IN
RELATED QUESTIONS
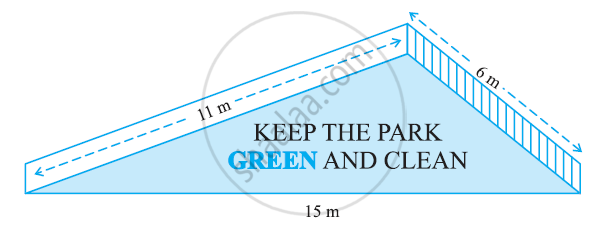
There is a slide in the park. One of its side walls has been painted in some colour with a message “KEEP THE PARK GREEN AND CLEAN” (see the given figure). If the sides of the wall are 15m, 11m, and 6m, find the area painted in colour.
The perimeter of an isosceles triangle is 42 cm and its baše is (32) times each of the equal sides. Find the length of each side of the triangle, area of the triangle and the height of the triangle.
Sides of a triangle are cm 45 cm, 39 cm and 42 cm, find its area.
Find the areas of the given plot. (All measures are in metres.)
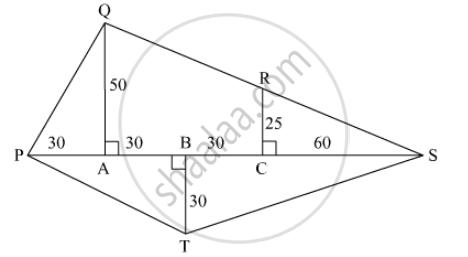
Find the areas of the given plot. (All measures are in metres.)
Determine whether the sets of points are collinear?
(a, b + c), (b, c + a) and (c, a + b)
The area of triangle formed by the points (− 5, 0), (0, – 5) and (5, 0) is
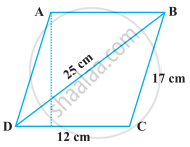
Find the area of a parallelogram given in figure. Also find the length of the altitude from vertex A on the side DC.
A field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.
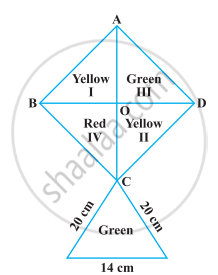
How much paper of each shade is needed to make a kite given in the following figure, in which ABCD is a square with diagonal 44 cm.