Advertisements
Advertisements
Question
A field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.
Solution
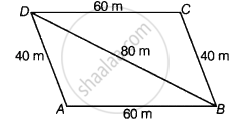
Let ABCD be a parallelogram field with sides AB = CD = 60 m, BC = DA = 40 m and diagonal BD = 80 m.
Area of parallelogram ABCD = 2(Area of ΔABD) ...(i)
In ΔABD,
Semi-perimeter of a triangle ΔABD,
`s = (a + b + c)/2`
= `(AB + BD + DA)/2`
= `(60 + 80 + 40)/2`
= `180/2`
= 90 m
∴ Area of ΔABD = `sqrt(s(s - a)(s - b)(s - c))` ...[By Heron’s formula]
= `sqrt(90(90 - 60)(90 - 80)(90 - 40))`
= `sqrt(90 xx 30 xx 10 xx 50)`
= `100 xx 3sqrt(15)`
= `300sqrt(15) m^2`
From equation (i),
Area of parallelogram ABCD = `2 xx 300sqrt(15) = 600sqrt(15) m^2`
Hence, the area of the parallelogram is `600sqrt(15) m^2`.
APPEARS IN
RELATED QUESTIONS
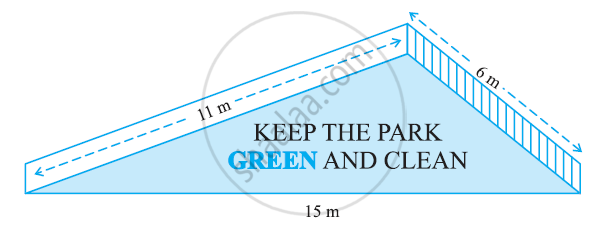
There is a slide in the park. One of its side walls has been painted in some colour with a message “KEEP THE PARK GREEN AND CLEAN” (see the given figure). If the sides of the wall are 15m, 11m, and 6m, find the area painted in colour.
The perimeter of an isosceles triangle is 42 cm and its baše is (32) times each of the equal sides. Find the length of each side of the triangle, area of the triangle and the height of the triangle.
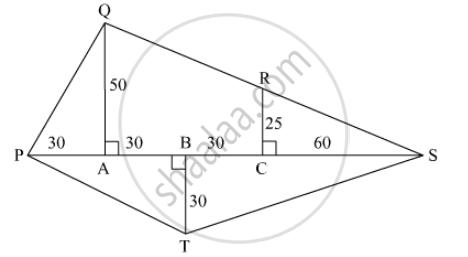
Find the areas of the given plot. (All measures are in metres.)
Determine whether the sets of points are collinear?
(a, b + c), (b, c + a) and (c, a + b)
Find the area of triangle AGF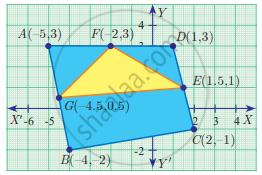
The area of a triangle is 5 sq. units. Two of its vertices are (2, 1) and (3, −2). The third vertex is (x, y) where y = x + 3. Find the coordinates of the third vertex.
Using Heron’s formula, find the area of a triangle whose sides are 10 cm, 24 cm, 26 cm
An isosceles right triangle has area 8 cm2. The length of its hypotenuse is ______.
The area of the isosceles triangle is `5/4 sqrt(11)` cm2, if the perimeter is 11 cm and the base is 5 cm.
The perimeter of an isosceles triangle is 32 cm. The ratio of the equal side to its base is 3 : 2. Find the area of the triangle.
