Advertisements
Advertisements
Question
The area of the isosceles triangle is `5/4 sqrt(11)` cm2, if the perimeter is 11 cm and the base is 5 cm.
Options
True
False
Solution
This statement is True.
Explanation:
Suppose that side of isosceles triangle be a.
Now, perimeter of an isosceles triangle:
2s = 5 + a + a ...[2s = a + b + c]
11 = 5 + 2a
2a = 11 – 5
2a = 6
a = 3
Now, the formula of an area of isosceles triangle = `a/4 sqrt(4b^2 - a^2)`
So, area of an isosceles triangle = `(5sqrt(4 xx (3)^2 - (5)^2))/4`
= `(5sqrt(4 xx 9 - 25))/4`
= `5 xx sqrt(36 - 25)/4`
= `(5sqrt(11))/4` cm2
APPEARS IN
RELATED QUESTIONS
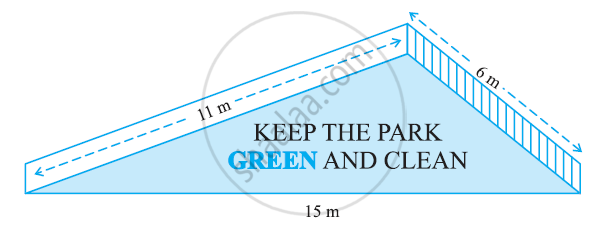
There is a slide in the park. One of its side walls has been painted in some colour with a message “KEEP THE PARK GREEN AND CLEAN” (see the given figure). If the sides of the wall are 15m, 11m, and 6m, find the area painted in colour.
Sides of a triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540 cm. Find its area.
The perimeter of an isosceles triangle is 42 cm and its baše is (32) times each of the equal sides. Find the length of each side of the triangle, area of the triangle and the height of the triangle.
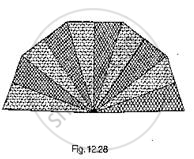
A hand fan is made by stitching lo equal size triangular strips of two different types of paper as shown in Fig. 12.28. The dimensions of equal strips are 25 cm, 25 cm and 14 cm. Find the area of each type of paper needed to make the hand fan.
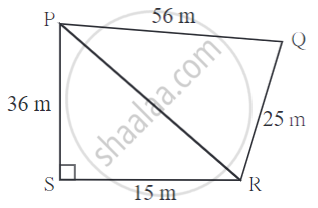
Look at the measures shown in the adjacent figure and find the area of ☐ PQRS.
A man walks near a wall, such that the distance between him and the wall is 10 units. Consider the wall to be the Y-axis. The path travelled by the man is
From a point in the interior of an equilateral triangle, perpendiculars are drawn on the three sides. The lengths of the perpendiculars are 14 cm, 10 cm and 6 cm. Find the area of the triangle.
A field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.
The perimeter of a triangular field is 420 m and its sides are in the ratio 6 : 7 : 8. Find the area of the triangular field.
How much paper of each shade is needed to make a kite given in the following figure, in which ABCD is a square with diagonal 44 cm.