Advertisements
Advertisements
Question
A hand fan is made by stitching lo equal size triangular strips of two different types of paper as shown in Fig. 12.28. The dimensions of equal strips are 25 cm, 25 cm and 14 cm. Find the area of each type of paper needed to make the hand fan.
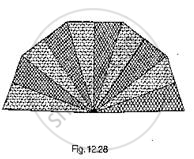
Solution
Given that the sides of ΔAOB are
AO = 24 cm
OB = 25 cm
BA = 14 cm
Area of each equal strips = Area of Δle AOB
Now, for area of ΔAOB
Perimeter of ΔAOB
Let 2s = AO + OB + BA
`⇒s=1/2(AO+OB+BA)`
`=1/2(25-25-14)=32 cm`
∴𝐵𝑦 𝑢𝑠𝑖𝑛𝑔 𝐻𝑒𝑟𝑜𝑛′𝑠𝑓𝑜𝑟𝑚𝑢𝑙𝑎𝑒
𝐴𝑟𝑒𝑎 𝑜𝑓 (Δ𝐴𝑂𝐵)=`sqrt(s(s-ao(s-ob)s-ba))`
`=sqrt(32(32-25)(32-25)(32-14))`
`=sqrt(32(7)(4)(18))`
`=168 cm^2`
∴ Area of each type of paper needed to make the hand fan = 5 ×(𝑎𝑟𝑒𝑎 𝑜𝑓 Δ𝐴𝑂𝐵)
= 5 × 168
= `840 cm^2`
APPEARS IN
RELATED QUESTIONS
An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.
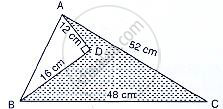
Find the area of the shaded region in the given figure.
The adjacent sides of a parallelogram ABCD measure 34 cm and 20 cm, and the diagonal AC measures 42 cm. Find the area of the parallelogram.
Determine whether the sets of points are collinear?
`(-1/2, 3), (-5, 6) and (-8, 8)`
If the points A(– 3, 9), B(a, b) and C(4, – 5) are collinear and if a + b = 1, then find a and b
Find the area of the unshaded region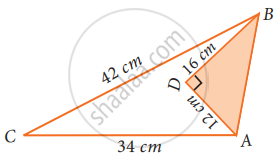
The perimeter of an equilateral triangle is 30 cm. The area is
The perimeter of an isosceles triangle is 32 cm. The ratio of the equal side to its base is 3 : 2. Find the area of the triangle.
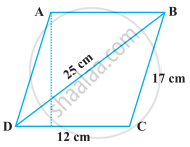
Find the area of a parallelogram given in figure. Also find the length of the altitude from vertex A on the side DC.
The sides of a quadrilateral ABCD are 6 cm, 8 cm, 12 cm and 14 cm (taken in order) respectively, and the angle between the first two sides is a right angle. Find its area.
