Advertisements
Advertisements
Question
An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.
Solution
Let the sides of an isosceles triangle be a = 12 cm, b = 12 cm, c = x cm
Since the perimeter of the triangle = 30 cm
∴ 12 cm + 12 cm + x cm = 30 cm
⇒ x = (30 − 24) = 6
Now, semi-perimeter, s = `30/2` cm = 15 cm
∴ Area of the triangle = `sqrt(s(s - a)(s - b)(s - c))`
= `sqrt(15(15-12)(15-12)(15-6)) cm^2`
= `sqrt(15 xx 3 xx 3 xx 9) cm^2`
= `sqrt(15 xx 3 xx 3 xx 3 xx 3 xx 3) cm^2`
= `sqrt(3^2 xx 3^2 xx 3 xx 5) cm^2`
= `3 xx 3 xx sqrt(3 xx 5) cm^2`
= `9sqrt15 cm^2`
Thus, the required area of the triangle is `9sqrt15 cm^2`.
APPEARS IN
RELATED QUESTIONS
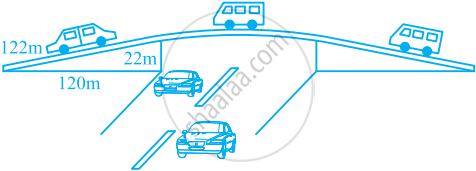
The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122m, 22m, and 120m (see the given figure). The advertisements yield an earning of ₹ 5000 per m2 per year. A company hired one of its walls for 3 months. How much rent did it pay?
The perimeter of a triangular field is 240 dm. If two of its sides are 78 dm and 50 dm, find the length of the perpendicular on the side of length 50 dm from the opposite vertex.
Find the area of an isosceles triangle having the base x cm and one side y cm.
Determine whether the sets of points are collinear?
`(-1/2, 3), (-5, 6) and (-8, 8)`
Find the area of triangle AGF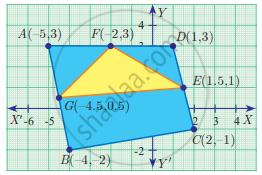
Find the area of triangle FED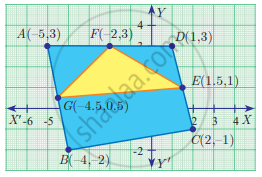
The semi-perimeter of a triangle having sides 15 cm, 20 cm and 25 cm is
The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 13 m, 14 m and 15 m. The advertisements yield an earning of Rs 2000 per m2 a year. A company hired one of its walls for 6 months. How much rent did it pay?
How much paper of each shade is needed to make a kite given in the following figure, in which ABCD is a square with diagonal 44 cm.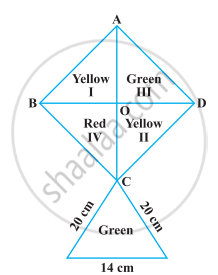
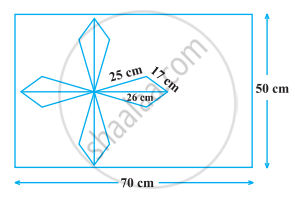
A design is made on a rectangular tile of dimensions 50 cm × 70 cm as shown in the following figure. The design shows 8 triangles, each of sides 26 cm, 17 cm and 25 cm. Find the total area of the design and the remaining area of the tile.