Advertisements
Advertisements
Question
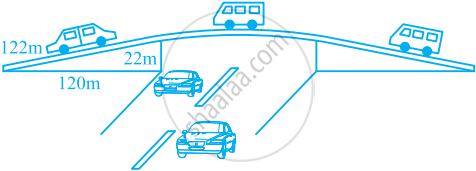
The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122m, 22m, and 120m (see the given figure). The advertisements yield an earning of ₹ 5000 per m2 per year. A company hired one of its walls for 3 months. How much rent did it pay?
Advertisements
Solution
The sides of the triangle (i.e., a, b, c) are 122 m, 22 m, and 120 m, respectively.
Perimeter of triangle = (122 + 22 + 120) m
2s = 264 m
s = 132 m
By Heron’s formula,
Area of triangle = `sqrt(s(s-a)(s-b)(s-c))`
Area of given triangle = `[sqrt(132(132-122)(132-22)(132-120))]m^2`
= `[sqrt(132(10)(110)(12))]m^2 = 1320m^2`
Rent of 1 m2 area per year = ₹ 5000
Rent of 1 m2 area per month = `₹ 5000/12`
Rent of 1320 m2 area for 3 months
= `₹ (5000/12xx3xx1320)`
= ₹ (5000 × 330)
= ₹ 16,50,000
Therefore, the company had to pay ₹ 16,50,000.
APPEARS IN
RELATED QUESTIONS
The perimeter of a triangle is 300 m. If its sides are in the ratio 3 : 5 : 7. Find the area of the triangle ?
The lengths of the sides of a triangle are in the ratio 3 : 4 : 5 and its perimeter is 144 cm. Find the area of the triangle and the height corresponding to the longest side.
Look at the measures shown in the adjacent figure and find the area of ☐ PQRS.
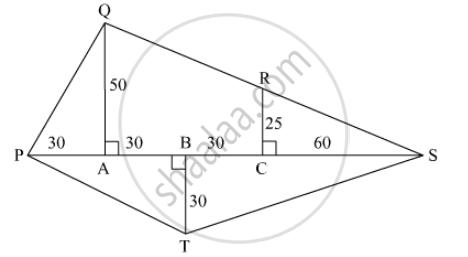
Find the areas of the given plot. (All measures are in metres.)
Find the area of the triangle formed by the points
(–10, –4), (–8, –1) and (–3, –5)
The area of a triangle is 5 sq. units. Two of its vertices are (2, 1) and (3, −2). The third vertex is (x, y) where y = x + 3. Find the coordinates of the third vertex.
Using Heron’s formula, find the area of a triangle whose sides are 1.8 m, 8 m, 8.2 m
The cost of levelling the ground in the form of a triangle having the sides 51 m, 37 m and 20 m at the rate of Rs 3 per m2 is Rs 918.
The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 13 m, 14 m and 15 m. The advertisements yield an earning of Rs 2000 per m2 a year. A company hired one of its walls for 6 months. How much rent did it pay?
Find the area of a parallelogram given in figure. Also find the length of the altitude from vertex A on the side DC.
