Advertisements
Advertisements
Question
A traffic signal board, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side ‘a’. Find the area of the signal board, using Heron’s formula. If its perimeter is 180 cm, what will be the area of the signal board?
Solution
The side of the traffic signal board = a
Perimeter of traffic signal board = 3 × a
2s = 3a ⇒ s = `3/2 a`
By heron's formula,
Area of triangle = `sqrt(s(s-a)(s-b)(s-c))`
Area of given triangle = `sqrt(3/2 a(3/2a-a)(3/2a-a)(3/2a-a))`
= `sqrt((3/2a)(a/2)(a/2)(a/2))`
= `sqrt3/4a^2` ... (1)
Perimeter of traffic signal board = 180 cm
Side of traffic signal board (a) = `(180/3) cm` = 60 cm
Using equation (1), the area of the traffic signal board
= `sqrt3/4(60cm)^2`
= `(3600/4sqrt3)cm^2` = `900sqrt3 cm^2`
APPEARS IN
RELATED QUESTIONS
The perimeter of a triangular field is 240 dm. If two of its sides are 78 dm and 50 dm, find the length of the perpendicular on the side of length 50 dm from the opposite vertex.
A triangle has sides 35 cm, 54 cm and 61 cm long. Find its area. Also, find the smallest of its altitudes ?
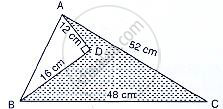
Find the area of the shaded region in the given figure.
Find the area of a quadrilateral ABCD in which AB = 42 cm, BC = 21 cm, CD = 29 cm, DA =34 cm and diagonal BD =20 cm.
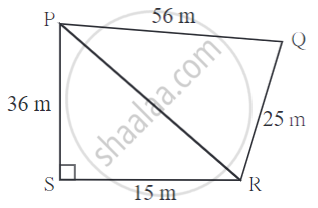
Look at the measures shown in the adjacent figure and find the area of ☐ PQRS.
If the points A(– 3, 9), B(a, b) and C(4, – 5) are collinear and if a + b = 1, then find a and b
The sides of the triangular ground are 22 m, 120 m and 122 m. Find the area and cost of levelling the ground at the rate of ₹ 20 per m2
The sides of a quadrilateral ABCD are 6 cm, 8 cm, 12 cm and 14 cm (taken in order) respectively, and the angle between the first two sides is a right angle. Find its area.
A rhombus shaped sheet with perimeter 40 cm and one diagonal 12 cm, is painted on both sides at the rate of Rs 5 per m2. Find the cost of painting.
The perimeter of a triangle is 50 cm. One side of a triangle is 4 cm longer than the smaller side and the third side is 6 cm less than twice the smaller side. Find the area of the triangle.
