Advertisements
Advertisements
प्रश्न
A traffic signal board, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side ‘a’. Find the area of the signal board, using Heron’s formula. If its perimeter is 180 cm, what will be the area of the signal board?
उत्तर
The side of the traffic signal board = a
Perimeter of traffic signal board = 3 × a
2s = 3a ⇒ s = `3/2 a`
By heron's formula,
Area of triangle = `sqrt(s(s-a)(s-b)(s-c))`
Area of given triangle = `sqrt(3/2 a(3/2a-a)(3/2a-a)(3/2a-a))`
= `sqrt((3/2a)(a/2)(a/2)(a/2))`
= `sqrt3/4a^2` ... (1)
Perimeter of traffic signal board = 180 cm
Side of traffic signal board (a) = `(180/3) cm` = 60 cm
Using equation (1), the area of the traffic signal board
= `sqrt3/4(60cm)^2`
= `(3600/4sqrt3)cm^2` = `900sqrt3 cm^2`
APPEARS IN
संबंधित प्रश्न
Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42 cm.
The perimeter of a triangle is 300 m. If its sides are in the ratio 3 : 5 : 7. Find the area of the triangle ?
The lengths of the sides of a triangle are in the ratio 3 : 4 : 5 and its perimeter is 144 cm. Find the area of the triangle and the height corresponding to the longest side.
Find the area of a triangle whose base and altitude are 5 cm and 4 cm respectively.
Sides of a triangle are cm 45 cm, 39 cm and 42 cm, find its area.
An advertisement board is in the form of an isosceles triangle with perimeter 36 m and each of the equal sides are 13 m. Find the cost of painting it at ₹ 17.50 per square metre.
A field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.
A rhombus shaped sheet with perimeter 40 cm and one diagonal 12 cm, is painted on both sides at the rate of Rs 5 per m2. Find the cost of painting.
How much paper of each shade is needed to make a kite given in the following figure, in which ABCD is a square with diagonal 44 cm.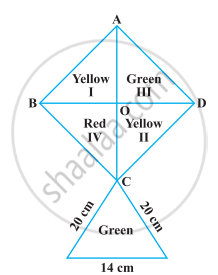
The perimeter of a triangle is 50 cm. One side of a triangle is 4 cm longer than the smaller side and the third side is 6 cm less than twice the smaller side. Find the area of the triangle.
