Advertisements
Advertisements
Question
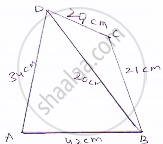
Find the area of a quadrilateral ABCD in which AB = 42 cm, BC = 21 cm, CD = 29 cm, DA =34 cm and diagonal BD =20 cm.
Solution
Given that
Sides of a quadrilateral are AB = 42 cm, BC = 21 cm, CD = 29 cm
DA = 34 cm and diagonal BD = 20 cm
Area of quadrilateral = area of ΔADB + area of ΔBCD.
Now, area of ΔABD
Perimeter of ΔABD
We know that
⇒ S = `1/2`(𝐴𝐵+𝐵𝐷+𝐷𝐴)
= `1/2`(34+42+20)=96
=`96/2`
= 48 𝑐𝑚
Area of ΔABD = `sqrt(S(S-AB)(S-BD)(S-DA))`
`=sqrt(48(48-42)(48-20)(48-34))`
`=sqrt(48(14)(6)(28)`
`=336cm^2`
Also for area of ΔBCD,
Perimeter of ΔBCD
`2s = BC + CD + BD`
`⇒S=1/2(29+21+20)+35cm`
By using heron’s formulae
Area of ΔBCD =`sqrt(s(s-bc)(s-cd)(s-db))`
`=sqrt(35(35-21)(53-29)(35-20))`
`=sqrt(210xx210)cm^2`
`= 210cm^2`
∴ Area of quadrilateral ABCD = 336 + 210 = 546 `cm^2`
APPEARS IN
RELATED QUESTIONS
Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42 cm.
An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.
Find the area of a triangle whose base and altitude are 5 cm and 4 cm respectively.
Sides of a triangle are cm 45 cm, 39 cm and 42 cm, find its area.
Find the area of the triangle formed by the points
(–10, –4), (–8, –1) and (–3, –5)
Determine whether the sets of points are collinear?
(a, b + c), (b, c + a) and (c, a + b)
Find the area of triangle FED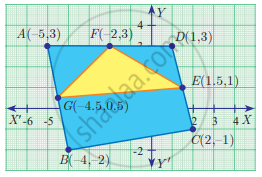
The area of a triangle is 5 sq. units. Two of its vertices are (2, 1) and (3, −2). The third vertex is (x, y) where y = x + 3. Find the coordinates of the third vertex.
Using Heron’s formula, find the area of a triangle whose sides are 10 cm, 24 cm, 26 cm
The area of the isosceles triangle is `5/4 sqrt(11)` cm2, if the perimeter is 11 cm and the base is 5 cm.
