Advertisements
Advertisements
Question
A rhombus shaped sheet with perimeter 40 cm and one diagonal 12 cm, is painted on both sides at the rate of Rs 5 per m2. Find the cost of painting.
Solution
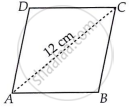
Let ABCD be a rhombus having sides AB = BC = CD = DA = x cm
Given that perimeter of a rhombus = 40 cm
`\implies` x + x + x + x = 40
`\implies` 4x = 40
`\implies x = 40/4`
∴ x = 10
In ΔABC, let a = AB = 10 cm, b = BC = 10 cm and c = AC = 12 cm
Now, semi-perimeter of a ΔABC,
`s = (a + b + c)/2`
= `((10 + 10 + 12)/2) cm`
= `32/2 cm`
= 16 cm
∴ Area of ΔABC = `sqrt(s(s - a)(s - b)(s - c))`
= `sqrt(16(16 - 10)(16 - 10)(16 - 12)) cm^2`
= `sqrt(16 xx 6 xx 6 xx 4) cm^2`
= 48 cm2
Now, area of the rhombus ABCD
= 2(Area of ΔABC)
= (2 × 48) cm2
= 96 cm2
∵ Cost of painting the sheet of 1 cm2 = Rs. 5
∴ Cost of painting the sheet of 96 cm2
= Rs. (96 × 5)
= Rs. 480
Thus, the cost of painting the sheet on both sides = Rs. (2 × 480) = Rs. 960
APPEARS IN
RELATED QUESTIONS
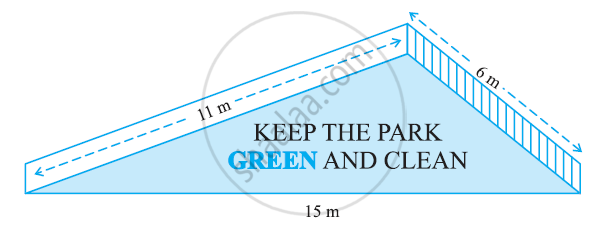
There is a slide in the park. One of its side walls has been painted in some colour with a message “KEEP THE PARK GREEN AND CLEAN” (see the given figure). If the sides of the wall are 15m, 11m, and 6m, find the area painted in colour.
Sides of a triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540 cm. Find its area.
A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 13 cm, 14 cm and 15 cm and the parallelogram stands on the base 14 cm, find the height of the parallelogram.
Find the area of a triangle formed by the lines 3x + y – 2 = 0, 5x + 2y – 3 = 0 and 2x – y – 3 = 0
Using Heron’s formula, find the area of a triangle whose sides are 10 cm, 24 cm, 26 cm
Using Heron’s formula, find the area of a triangle whose sides are 1.8 m, 8 m, 8.2 m
An advertisement board is in the form of an isosceles triangle with perimeter 36 m and each of the equal sides are 13 m. Find the cost of painting it at ₹ 17.50 per square metre.
If the side of a rhombus is 10 cm and one diagonal is 16 cm, the area of the rhombus is 96 cm2.
How much paper of each shade is needed to make a kite given in the following figure, in which ABCD is a square with diagonal 44 cm.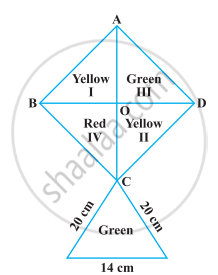
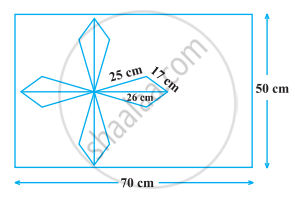
A design is made on a rectangular tile of dimensions 50 cm × 70 cm as shown in the following figure. The design shows 8 triangles, each of sides 26 cm, 17 cm and 25 cm. Find the total area of the design and the remaining area of the tile.