Advertisements
Advertisements
Question
Using Heron’s formula, find the area of a triangle whose sides are 1.8 m, 8 m, 8.2 m
Solution
Here a = 1.8 m, b = 8 m, c = 8.2 m
s = `("a" + "b" + "c")/2`
= `((1.8 + 8 + 8.2)"m")/2`
= `18/2`
= 9 m
s – a = 9 – 1.8 = 7.2 m
s – b = 9 – 8 = 1 m
s – c = 9 – 8.2 m = 0.8
Area of triangle
= `sqrt("s"("s" - "a")("s" - "b")("s" - "c"))`
= `sqrt(9 xx 7.2 xx 1 xx 0.8)`
= `sqrt(9 xx 5.76)`
= `sqrt9 xx sqrt(576/100)`
= `3 xx 24/10`
= 3 × 2.4
= 7.2 m2
∴ Area of the triangle = 7.2 sq.m
APPEARS IN
RELATED QUESTIONS
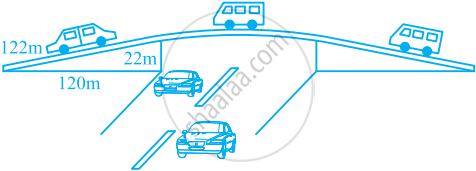
The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122m, 22m, and 120m (see the given figure). The advertisements yield an earning of ₹ 5000 per m2 per year. A company hired one of its walls for 3 months. How much rent did it pay?
Sides of a triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540 cm. Find its area.
The adjacent sides of a parallelogram ABCD measure 34 cm and 20 cm, and the diagonal AC measures 42 cm. Find the area of the parallelogram.
Find the area of an isosceles triangle having the base x cm and one side y cm.
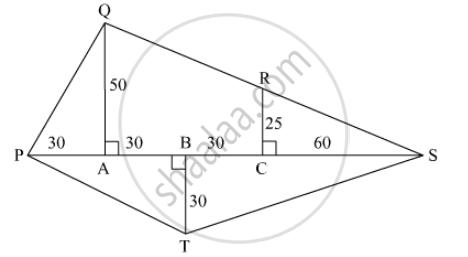
Find the areas of the given plot. (All measures are in metres.)
Find the area of the triangle formed by the points
(1, – 1), (– 4, 6) and (– 3, – 5)
The area of a triangle is 5 sq. units. Two of its vertices are (2, 1) and (3, −2). The third vertex is (x, y) where y = x + 3. Find the coordinates of the third vertex.
Using Heron’s formula, find the area of a triangle whose sides are 10 cm, 24 cm, 26 cm
Find the area of an equilateral triangle whose perimeter is 180 cm
The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 13 m, 14 m and 15 m. The advertisements yield an earning of Rs 2000 per m2 a year. A company hired one of its walls for 6 months. How much rent did it pay?
