Advertisements
Advertisements
Question
The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 13 m, 14 m and 15 m. The advertisements yield an earning of Rs 2000 per m2 a year. A company hired one of its walls for 6 months. How much rent did it pay?
Solution
Let the sides of a triangular walls are a = 13 m, b = 14 m and c = 15 m.
Now, the semi-perimeter of triangular side wall,
`s = (a + b + c)/2`
= `(13 + 14 + 15)/2`
= 21 m
Now, area of triangular wall = `sqrt(s(s - a)(s - b)(s - c))` ...[By Heron’s formula]
= `sqrt(21(21 - 13)(21 - 14)(21 - 15))`
= `sqrt(21 xx (21 - 13) xx (21 - 14) xx (21 - 15))`
= `sqrt(21 xx 8 xx 7 xx 6)`
= `sqrt(21 xx 4 xx 2 xx 7 xx 3 xx 2)`
= `sqrt(21^2 xx 4^2)`
= 21 × 4
= 84 m2
The advertisement yield earning per year for 1 m2 area is Rs. 2000.
Therefore, advertisement yield earning per year on 84 m2 = 2000 × 84 = Rs. 168000.
According to the question, the company hired one of its walls for 6 months, therefore company pay the rent = `1/2 xx 168000` = Rs. 84000.
Hence, the company paid rent Rs. 84000.
APPEARS IN
RELATED QUESTIONS
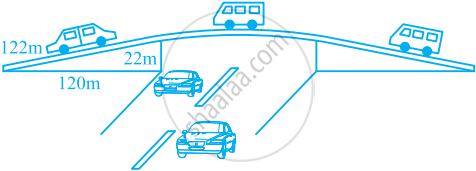
The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122m, 22m, and 120m (see the given figure). The advertisements yield an earning of ₹ 5000 per m2 per year. A company hired one of its walls for 3 months. How much rent did it pay?
Find the area of a triangle whose base and altitude are 5 cm and 4 cm respectively.
Find the areas of the given plot. (All measures are in metres.)
The perimeter of a triangular plot is 600 m. If the sides are in the ratio 5 : 12 : 13, then find the area of the plot
Find the area of the unshaded region
An isosceles right triangle has area 8 cm2. The length of its hypotenuse is ______.
The cost of levelling the ground in the form of a triangle having the sides 51 m, 37 m and 20 m at the rate of Rs 3 per m2 is Rs 918.
How much paper of each shade is needed to make a kite given in the following figure, in which ABCD is a square with diagonal 44 cm.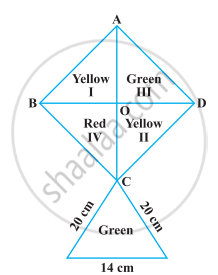
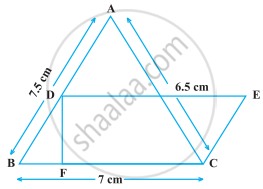
In the following figure, ∆ABC has sides AB = 7.5 cm, AC = 6.5 cm and BC = 7 cm. On base BC a parallelogram DBCE of same area as that of ∆ABC is constructed. Find the height DF of the parallelogram.
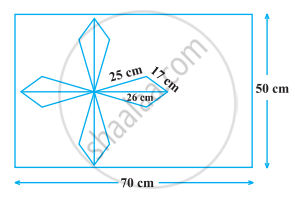
A design is made on a rectangular tile of dimensions 50 cm × 70 cm as shown in the following figure. The design shows 8 triangles, each of sides 26 cm, 17 cm and 25 cm. Find the total area of the design and the remaining area of the tile.