Advertisements
Advertisements
Question
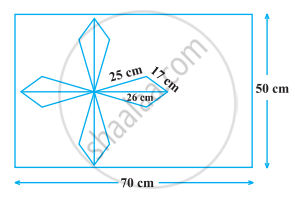
A design is made on a rectangular tile of dimensions 50 cm × 70 cm as shown in the following figure. The design shows 8 triangles, each of sides 26 cm, 17 cm and 25 cm. Find the total area of the design and the remaining area of the tile.
Solution
Given, the dimension of rectangular tile is 50 cm × 70 cm.
∴ Area of rectangular tile = 50 × 70 = 3500 cm2
The sides of a design of one triangle be
a = 25 cm, b = 17 cm and c = 26 cm
Now, semi-perimeter,
`s = (a + b + c)/2`
= `(25 + 17 + 26)/2`
= `68/2`
= 34
∴ Area of one triangle = `sqrt(s(s - a)(s - b)(s - c))` ...[By Heron’s formula]
= `sqrt(34 xx 9 xx 17 xx 8)`
= `sqrt(17 xx 2 xx 3 xx 3 xx 17 xx 2 xx 2 xx 2)`
= 17 × 3 × 2 × 2
= 204 cm2
∴ Total area of eight triangles = 204 × 8 = 1632 cm2
Now, area of the design = Total area of eight triangles
= 1632 cm2
Also, remaining area of the tile = Area of the rectangle – Area of the design
= 3500 – 1632
= 1868 cm2
Hence, the total area of the design is 1632 cm2 and the remaining area of the tile is 1868 cm2.
APPEARS IN
RELATED QUESTIONS
A traffic signal board, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side ‘a’. Find the area of the signal board, using Heron’s formula. If its perimeter is 180 cm, what will be the area of the signal board?
Find the area of the shaded region in the given figure.
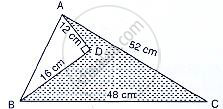
Find the area of a quadrilateral ABCD in which AB = 42 cm, BC = 21 cm, CD = 29 cm, DA =34 cm and diagonal BD =20 cm.
Find the area of a triangle whose base and altitude are 5 cm and 4 cm respectively.
Find the area of the triangle formed by the points
(–10, –4), (–8, –1) and (–3, –5)
If the points A(– 3, 9), B(a, b) and C(4, – 5) are collinear and if a + b = 1, then find a and b
The area of a triangle is 5 sq. units. Two of its vertices are (2, 1) and (3, −2). The third vertex is (x, y) where y = x + 3. Find the coordinates of the third vertex.
The area of the isosceles triangle is `5/4 sqrt(11)` cm2, if the perimeter is 11 cm and the base is 5 cm.
The cost of levelling the ground in the form of a triangle having the sides 51 m, 37 m and 20 m at the rate of Rs 3 per m2 is Rs 918.
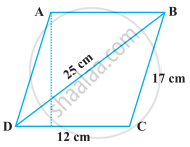
Find the area of a parallelogram given in figure. Also find the length of the altitude from vertex A on the side DC.