Advertisements
Advertisements
Question
The dimensions of a rectangle ABCD are 51 cm × 25 cm. A trapezium PQCD with its parallel sides QC and PD in the ratio 9 : 8, is cut off from the rectangle as shown in the following figure. If the area of the trapezium PQCD is `5/6` th part of the area of the rectangle, find the lengths QC and PD.

Solution
Given: ABCD is a rectangle, where AB = 51 cm and BC = 25 cm.
The parallel sides QC and PD of the trapezium PQCD are in the ratio of 9 : 8. Let QC = 9x and PD = 8x.
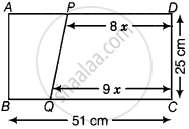
Now, the area of trapezium PQCD:
= `1/2` × (Sum of parallel sides) × (Distance between parallel sides)
= `1/2 xx (9x + 8x) xx 25 cm^2`
= `1/2 xx 17x xx 25`
Again, area of rectangle ABCD = BC × CD = 51 × 25
Now, according to the question,
Area of trapezium PQCD = `5/6` × Area of rectangle ABCD
= `1/2 xx 17x xx 25`
= `5/6 xx 51 xx 25`
x = `5/6 xx 51 xx 25 xx 2xx 1/(17 xx 25)`
x = 5
Therefore, the length of the trapezium PQCD, QC = 9x = 9 × 5 = 45 cm and PD = 8x = 8 × 5 = 40 cm.
APPEARS IN
RELATED QUESTIONS
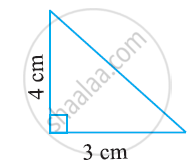
Find the area of the following triangle:
Find the area of a triangle whose vertices are
(a, c + a), (a, c) and (−a, c − a)
Prove that the points (2a, 4a), (2a, 6a) and `(2a + sqrt3a, 5a)` are the vertices of an equilateral triangle.
If `a≠ b ≠ c`, prove that the points (a, a2), (b, b2), (c, c2) can never be collinear.
Find the area of Δ ABC whose vertices are:
A (1,2) B (-2,3) and C (-3,-4)
If the points P(-3, 9), Q(a, b) and R(4, -5) are collinear and a+b=1, find the value of a and b.
Find the value of p for which the points (−5, 1), (1, p) and (4, −2) are collinear.
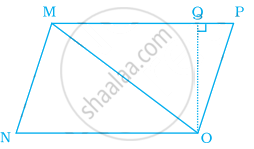
Area of triangle MNO in the figure is ______.
Area of triangle PQR is 100 cm2 as shown in the below figure. If altitude QT is 10 cm, then its base PR is ______.

Ratio of the area of ∆WXY to the area of ∆WZY is 3:4 in the given figure. If the area of ∆WXZ is 56 cm2 and WY = 8 cm, find the lengths of XY and YZ.

