Advertisements
Advertisements
प्रश्न
The dimensions of a rectangle ABCD are 51 cm × 25 cm. A trapezium PQCD with its parallel sides QC and PD in the ratio 9 : 8, is cut off from the rectangle as shown in the following figure. If the area of the trapezium PQCD is `5/6` th part of the area of the rectangle, find the lengths QC and PD.

उत्तर
Given: ABCD is a rectangle, where AB = 51 cm and BC = 25 cm.
The parallel sides QC and PD of the trapezium PQCD are in the ratio of 9 : 8. Let QC = 9x and PD = 8x.
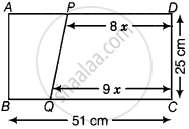
Now, the area of trapezium PQCD:
= `1/2` × (Sum of parallel sides) × (Distance between parallel sides)
= `1/2 xx (9x + 8x) xx 25 cm^2`
= `1/2 xx 17x xx 25`
Again, area of rectangle ABCD = BC × CD = 51 × 25
Now, according to the question,
Area of trapezium PQCD = `5/6` × Area of rectangle ABCD
= `1/2 xx 17x xx 25`
= `5/6 xx 51 xx 25`
x = `5/6 xx 51 xx 25 xx 2xx 1/(17 xx 25)`
x = 5
Therefore, the length of the trapezium PQCD, QC = 9x = 9 × 5 = 45 cm and PD = 8x = 8 × 5 = 40 cm.
APPEARS IN
संबंधित प्रश्न
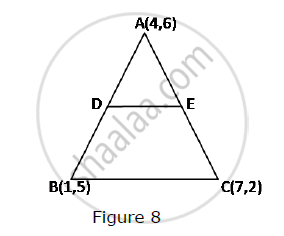
In Fig. 8, the vertices of ΔABC are A(4, 6), B(1, 5) and C(7, 2). A line-segment DE is drawn to intersect the sides AB and AC at D and E respectively such that `(AD)/(AB)=(AE)/(AC)=1/3 `Calculate th area of ADE and compare it with area of ΔABCe.
If A(4, –6), B(3, –2) and C(5, 2) are the vertices of ∆ABC, then verify the fact that a median of a triangle ABC divides it into two triangle of equal areas.
Find the missing value:
| Base | Height | Area of triangle |
| 15 cm | ______ | 87 cm2 |
If `a≠ b ≠ c`, prove that the points (a, a2), (b, b2), (c, c2) can never be collinear.
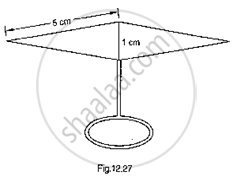
Find the area of the blades of thc magnetic compass shown in Fig.. 12.27. (Take √11 = 3.32).
What is the area of a triangle with base 4.8 cm and height 3.6 cm?
The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| ? | 12 m | 24 sq.m |
Let `Delta = abs (("x", "y", "z"),("x"^2, "y"^2, "z"^2),("x"^3, "y"^3, "z"^3)),` then the value of `Delta` is ____________.
Ratio of areas of ∆MNO, ∆MOP and ∆MPQ in the given figure is ______.

Let a vector `αhati + βhatj` be obtained by rotating the vector `sqrt(3)hati + hatj` by an angle 45° about the origin in counter-clockwise direction in the first quadrant. Then the area of triangle having vertices (α, β), (0, β) and (0, 0) is equal to ______.
