Advertisements
Advertisements
Question
Area of triangle MNO in the figure is ______.
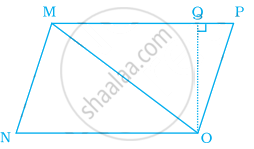
Options
`1/2` MN × NO
`1/2` NO × MO
`1/2` MN × OQ
`1/2` NO × OQ
Solution
Area of triangle MNO in the figure is `underlinebb(1/2 NO xx OQ)`.
Explanation:

MNO is a triangle
We know that, area of triangle = `1/2` (base × height)
= `1/2` × NO × OQ
APPEARS IN
RELATED QUESTIONS
If the points A(−2, 1), B(a, b) and C(4, −1) are collinear and a − b = 1, find the values of a and b.
ΔABC is isosceles with AB = AC = 7.5 cm and BC = 9 cm (see the given figure). The height AD from A to BC, is 6 cm. Find the area of ΔABC. What will be the height from C to AB i.e., CE?

Find the area of the quadrilaterals, the coordinates of whose vertices are
(−3, 2), (5, 4), (7, −6) and (−5, −4)
Find the area of the quadrilaterals, the coordinates of whose vertices are
(1, 2), (6, 2), (5, 3) and (3, 4)
Show that the points are the vertices of an isosceles right triangle.
Find the third vertex of a ΔABC if two of its vertices are B(-3,1) and C (0,-2) and its centroid is at the origin
Show that the points A (3,1) , B (0,-2) , C(1,1) and D (4,4) are the vertices of parallelogram ABCD.
Find the value of x for which points A(x, 2), B(-3, -4) and C(7, -5) are collinear.
If A, B, C are the angles of a triangle, then ∆ = `|(sin^2"A", cot"A", 1),(sin^2"B", cot"B", 1),(sin^2"C", cot"C", 1)|` = ______.
If `D((-1)/2, 5/2), E(7, 3)` and `F(7/2, 7/2)` are the midpoints of sides of ∆ABC, find the area of the ∆ABC.
