Advertisements
Advertisements
Question
Find the value of x for which points A(x, 2), B(-3, -4) and C(7, -5) are collinear.
Solution
` "Let" A(x_1,y_1) = A(x,2) ,B (x_2,y_2)=B(-3,-4) and (x_3,y_3) = c=(7,-5) `.So the condition for three collinear points is
`x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)=0`
⇒ x(-4+5)-3(-5-2)+7(2+4)=0
⇒ x+21+42=0
⇒ x=-63
Hence , x= -63
APPEARS IN
RELATED QUESTIONS
Find the area of the quadrilateral ABCD whose vertices are respectively A(1, 1), B(7, –3), C(12, 2) and D(7, 21).
For what value of x will the points (x, –1), (2, 1) and (4, 5) lie on a line ?
If area of triangle is 35 square units with vertices (2, −6), (5, 4), and (k, 4), then k is ______.
Four points A (6, 3), B (−3, 5), C(4, −2) and D (x, 3x) are given in such a way that `(ΔDBG) /(ΔABG)=1/2,` find x
In a ΔABC, AB = 15 cm, BC = 13 cm and AC = 14 cm. Find the area of ΔABC and hence its altitude on AC ?
For what values of k are the points A(8, 1) B(3, -2k) and C(k, -5) collinear.
Find the value(s) of p for which the points (3p + 1, p), (p + 2, p – 5) and (p + 1, –p) are collinear ?
Let ∆ = `|("A"x, x^2, 1),("B"y, y^2, 1),("C"z, z^2, 1)|`and ∆1 = `|("A", "B", "C"),(x, y, z),(zy, zx, xy)|`, then ______.
The points A(2, 9), B(a, 5) and C(5, 5) are the vertices of a triangle ABC right angled at B. Find the values of a and hence the area of ∆ABC.
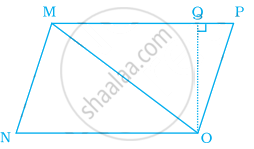
Area of triangle MNO in the figure is ______.