Advertisements
Advertisements
प्रश्न
Find the value of x for which points A(x, 2), B(-3, -4) and C(7, -5) are collinear.
उत्तर
` "Let" A(x_1,y_1) = A(x,2) ,B (x_2,y_2)=B(-3,-4) and (x_3,y_3) = c=(7,-5) `.So the condition for three collinear points is
`x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)=0`
⇒ x(-4+5)-3(-5-2)+7(2+4)=0
⇒ x+21+42=0
⇒ x=-63
Hence , x= -63
APPEARS IN
संबंधित प्रश्न
Find a relation between x and y if the points (x, y), (1, 2) and (7, 0) are collinear.
If A(–5, 7), B(–4, –5), C(–1, –6) and D(4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD
Two vertices of a triangle are (1, 2), (3, 5) and its centroid is at the origin. Find the coordinates of the third vertex.
Show that the points are the vertices of an isosceles right triangle.
For what value of k(k>0) is the area of the triangle with vertices (-2, 5), (k, -4) and (2k+1, 10) equal to 53 square units?
If the points P(-3, 9), Q(a, b) and R(4, -5) are collinear and a+b=1, find the value of a and b.
The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| 20 cm | 40 cm | ? |
In the given figure, ratio of the area of triangle ABC to the area of triangle ACD is the same as the ratio of base BC of triangle ABC to the base CD of ΔACD.

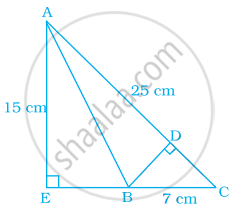
In the given figure, triangle AEC is right-angled at E, B is a point on EC, BD is the altitude of triangle ABC, AC = 25 cm, BC = 7 cm and AE = 15 cm. Find the area of triangle ABC and the length of DB.
Using determinants, find the area of ΔPQR with vertices P(3, 1), Q(9, 3) and R(5, 7). Also, find the equation of line PQ using determinants.
