Advertisements
Advertisements
प्रश्न
Find a relation between x and y if the points (x, y), (1, 2) and (7, 0) are collinear.
उत्तर
If the given points are collinear, then the area of triangle formed by these points will be 0.
Area of Triangle = `1/2 {x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)}`
Area = `1/2[x(2-0)+1(0-y)+7(y-2)]`
`0=1/2[2x-y+7y-14]`
`0=1/2[2x+6y-14]`
2x+6y-14=0
x+3y-7 =0
This is the required relation between x and y.
APPEARS IN
संबंधित प्रश्न
Find the area of a triangle whose vertices are A(3, 2), B (11, 8) and C(8, 12).
For what value of k are the points (k, 2 – 2k), (–k + 1, 2k) and (–4 – k, 6 – 2k) are collinear ?
Prove analytically that the line segment joining the middle points of two sides of a triangle is equal to half of the third side.
For what value of y, are the points P(1, 4), Q(3,y) and R(-3, 16) are collinear ?
Find the area of ΔABC with vertices A(0, -1), B(2,1) and C(0, 3). Also, find the area of the triangle formed by joining the midpoints of its sides. Show that the ratio of the areas of two triangles is 4:1.
Find the value of p for which the points (−5, 1), (1, p) and (4, −2) are collinear.
If the co-ordinates of the vertices of an equilateral triangle with sides of length ‘a’ are (x1, y1), (x2, y2), (x3, y3), then `|(x_1, y_1, 1),(x_2, y_2, 1),(x_3, y_3, 1)|^2 = (3"a"^4)/4`
A(6, 1), B(8, 2) and C(9, 4) are three vertices of a parallelogram ABCD. If E is the midpoint of DC, find the area of ∆ADE.
Find the area of the triangle whose vertices are (–8, 4), (–6, 6) and (–3, 9).
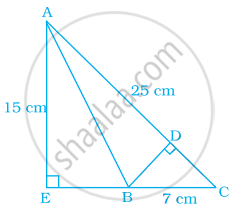
In the given figure, triangle AEC is right-angled at E, B is a point on EC, BD is the altitude of triangle ABC, AC = 25 cm, BC = 7 cm and AE = 15 cm. Find the area of triangle ABC and the length of DB.