Advertisements
Advertisements
Question
Find a relation between x and y if the points (x, y), (1, 2) and (7, 0) are collinear.
Solution
If the given points are collinear, then the area of triangle formed by these points will be 0.
Area of Triangle = `1/2 {x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)}`
Area = `1/2[x(2-0)+1(0-y)+7(y-2)]`
`0=1/2[2x-y+7y-14]`
`0=1/2[2x+6y-14]`
2x+6y-14=0
x+3y-7 =0
This is the required relation between x and y.
APPEARS IN
RELATED QUESTIONS
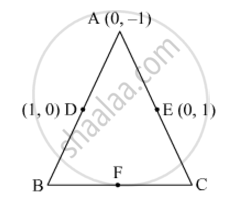
In Fig. 6, ABC is a triangle coordinates of whose vertex A are (0, −1). D and E respectively are the mid-points of the sides AB and AC and their coordinates are (1, 0) and (0, 1) respectively. If F is the mid-point of BC, find the areas of ∆ABC and ∆DEF.
Find the area of the triangle ABC with A(1, −4) and mid-points of sides through A being (2, −1) and (0, −1).
If the points A(x, 2), B(−3, −4) and C(7, − 5) are collinear, then the value of x is:
(A) −63
(B) 63
(C) 60
(D) −60
The vertices of ∆ABC = are A (4, 6), B(1, 5) and C(7, 2). A line is drawn to intersect sides AB and AC at D and E respectively such that `\frac{AD}{AB}=\frac{AE}{AC}=\frac{1}{4}` .Calculate the area of ∆ADE and compare it with the area of ∆ABC
Find the area of a triangle with vertices at the point given in the following:
(−2, −3), (3, 2), (−1, −8)
If area of triangle is 35 square units with vertices (2, −6), (5, 4), and (k, 4), then k is ______.
If A(–5, 7), B(–4, –5), C(–1, –6) and D(4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD
Find the area of a triangle whose vertices are
(a, c + a), (a, c) and (−a, c − a)
Prove that (2, -2) (-2, 1) and (5, 2) are the vertices of a right-angled triangle. Find the area of the triangle and the length of the hypotenuse.
The area of a triangle with vertices A, B, C is given by ______.
