Question

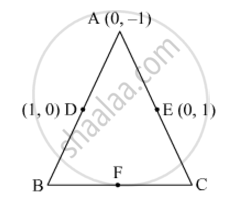
In Fig. 6, ABC is a triangle coordinates of whose vertex A are (0, −1). D and E respectively are the mid-points of the sides AB and AC and their coordinates are (1, 0) and (0, 1) respectively. If F is the mid-point of BC, find the areas of ∆ABC and ∆DEF.

Answer 1

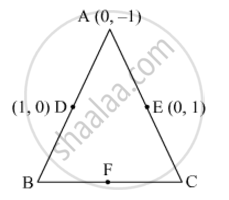
Let the coordinates of B and C be (x₂, y₂) and (x₃, y₃), respectively.

D is the midpoint of AB.

So,

`(1,0)=((x_2+0)/2,(y_2-1)/2)`

`=>1 = x_2/2 `

⇒ x₂ = 2 and y₂ = 1

Thus, the coordinates of B are (2, 1).

Similarly, E is the midpoint of AC.

So,

`(0,1)=((x_3+0)/2, (y_3-1)/2)`

`=>0=x_3/2 `

⇒ x₃ = 0 and y₃ = 3

Thus, the coordinates of C are (0, 3).

Also, F is the midpoint of BC. So, its coordinates are 

`((2+0)/2,(1+3)/2)=(1,2)`

Now,

Area of a triangle = `1/2`[x₁(y₂−y₃)+x₂(y₃−y₁)+x₃(y₁−y₂)]

Thus, the area of ∆ABC is 

`1/2[0(1-3)+2(3+1)+0(-1-1)]`

`=1/2xx8`

=4 square units

And the area of ∆DEF is

`1/2`[1(1−2)+0(2−0)+1(0−1)]

`=1/2xx(-2)`

=1 square unit     (Taking the numerical value, as the area cannot be negative)