Advertisements
Advertisements
प्रश्न
For what value of y, are the points P(1, 4), Q(3,y) and R(-3, 16) are collinear ?
उत्तर
P(1, 4), Q(3,y) and R(-3, 16) are the given points. Then:
`(x_1=1, y_1=4), (x_2=3, y_2=y) and (x_3 =-3, y_3 =16)`
It is given that the points P, Q and R are collinear. Therefor,
`x_1 (y_2-y_3) +x_2(y_3-y_1)+x_3(y_1-y_2)=0`
`⇒ 1(y-16)+3(16-4)+(-3)(4-y)=0`
`⇒ 1(y-16)+3(12)-3(4-y)=0`
`⇒ y-16+36-12+3y=0`
`⇒8+4y=0`
`⇒ 4y =-8/4=-2`
When, y=-2 the given points are collinear.
APPEARS IN
संबंधित प्रश्न
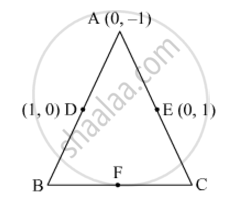
In Fig. 6, ABC is a triangle coordinates of whose vertex A are (0, −1). D and E respectively are the mid-points of the sides AB and AC and their coordinates are (1, 0) and (0, 1) respectively. If F is the mid-point of BC, find the areas of ∆ABC and ∆DEF.
The vertices of ∆ABC = are A (4, 6), B(1, 5) and C(7, 2). A line is drawn to intersect sides AB and AC at D and E respectively such that `\frac{AD}{AB}=\frac{AE}{AC}=\frac{1}{4}` .Calculate the area of ∆ADE and compare it with the area of ∆ABC
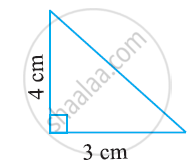
Find the area of the following triangle:
Find the area of a triangle whose vertices are
(6,3), (-3,5) and (4,2)
Find the centroid of ΔABC whose vertices are A(-1, 0) B(5, -2) and C(8,2)
Show that the points A (3,1) , B (0,-2) , C(1,1) and D (4,4) are the vertices of parallelogram ABCD.
Find the area of ΔABC whose vertices are:
A( 3,8) , B(-4,2) and C( 5, -1)
What is the area of a triangle with base 4.8 cm and height 3.6 cm?
The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| ? | 12 m | 24 sq.m |
The value of the determinant `abs((1,"x","x"^3),(1,"y","y"^3),(1,"z","z"^3))` is ____________.
