Advertisements
Advertisements
Question
Let ∆ = `|("A"x, x^2, 1),("B"y, y^2, 1),("C"z, z^2, 1)|`and ∆1 = `|("A", "B", "C"),(x, y, z),(zy, zx, xy)|`, then ______.
Options
∆1 = – ∆
∆ ≠ ∆1
∆ – ∆1 = 0
None of these
Solution
Let ∆ = `|("A"x, x^2, 1),("B"y, y^2, 1),("C"z, z^2, 1)|`and ∆1 = `|("A", "B", "C"),(x, y, z),(zy, zx, xy)|`, then ∆ – ∆1 = 0.
Explanation:
∆1 = `|("A", "B", "C"),(x, y, z),(zy, zx, xy)|`
= `|("A", x, yz),("B", y, zx),("C", z, xy)|`
= `1/(xyz) |("A"x, x^2, xyz),("B"y, y^2, xyz),("C"z, z^2, xyz)|`
= `(xyz)/(xyz)|("A"x, x^2, 1),("B"y, y^2, 1),("C"z, z^2, 1)|`
= ∆
APPEARS IN
RELATED QUESTIONS
If A(4, –6), B(3, –2) and C(5, 2) are the vertices of ∆ABC, then verify the fact that a median of a triangle ABC divides it into two triangle of equal areas.
Prove that the points (a, b + c), (b, c + a) and (c, a + b) are collinear
Find the area of the triangle whose vertices are: (2, 3), (-1, 0), (2, -4)
In each of the following find the value of 'k', for which the points are collinear.
(7, -2), (5, 1), (3, -k)
Find the area of the quadrilateral whose vertices, taken in order, are (-4, -2), (-3, -5), (3, -2) and (2, 3).
Find the centre of a circle passing through the points (6, − 6), (3, − 7) and (3, 3).
Show that points A (a, b + c), B (b, c + a), C (c, a + b) are collinear.
Find values of k if area of triangle is 4 square units and vertices are (−2, 0), (0, 4), (0, k)
The area of a triangle is 5 sq units. Two of its vertices are (2, 1) and (3, –2). If the third vertex is (`7/2`, y). Find the value of y
Find the area of the quadrilaterals, the coordinates of whose vertices are
(−3, 2), (5, 4), (7, −6) and (−5, −4)
The area of a triangle is 5. Two of its vertices are (2, 1) and (3, −2). The third vertex lies on y = x + 3. Find the third vertex.
Find the angle subtended at the origin by the line segment whose end points are (0, 100) and (10, 0).
If the coordinates of the mid-points of the sides of a triangle are (3, 4) (4, 6) and (5, 7), find its vertices.
Prove that the points A(2, 4), b(2, 6) and (2 +`sqrt(3)` ,5) are the vertices of an equilateral triangle
Show that the points (-3, -3),(3,3) and C (-3 `sqrt(3) , 3 sqrt(3))` are the vertices of an equilateral triangle.
Show that the points O(0,0), A`( 3,sqrt(3)) and B (3,-sqrt(3))` are the vertices of an equilateral triangle. Find the area of this triangle.
Find the value of y for which the points A(-3, 9), B(2,y) and C(4,-5) are collinear.
Find a relation between x and y, if the points A(x, y), B(-5, 7) and C(-4, 5) are collinear.
Find the value(s) of k so that the quadratic equation x2 − 4kx + k = 0 has equal roots.
If the co-ordinates of the vertices of an equilateral triangle with sides of length ‘a’ are (x1, y1), (x2, y2), (x3, y3), then `|(x_1, y_1, 1),(x_2, y_2, 1),(x_3, y_3, 1)|^2 = (3"a"^4)/4`
If the points (2, -3), (k, -1), and (0, 4) are collinear, then find the value of 4k.
The points (1,1), (-2, 7) and (3, -3) are ______.
The points (0, 5), (0, –9) and (3, 6) are collinear.
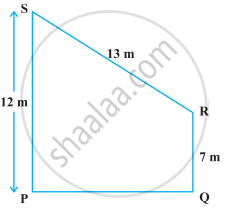
Find the area of the trapezium PQRS with height PQ given in the following figure.
A rectangular plot is given for constructing a house, having a measurement of 40 m long and 15 m in the front. According to the laws, a minimum of 3 m, wide space should be left in the front and back each and 2 m wide space on each of other sides. Find the largest area where house can be constructed.
The dimensions of a rectangle ABCD are 51 cm × 25 cm. A trapezium PQCD with its parallel sides QC and PD in the ratio 9 : 8, is cut off from the rectangle as shown in the following figure. If the area of the trapezium PQCD is `5/6` th part of the area of the rectangle, find the lengths QC and PD.

Area of a right-angled triangle is 30 cm2. If its smallest side is 5 cm, then its hypotenuse is ______.
Area of a triangle = `1/2` base × ______.
In the given figure, ratio of the area of triangle ABC to the area of triangle ACD is the same as the ratio of base BC of triangle ABC to the base CD of ΔACD.

Triangles having the same base have equal area.
