Advertisements
Advertisements
Question
Find the angle subtended at the origin by the line segment whose end points are (0, 100) and (10, 0).
Solution
Let the given points be A(0,100), B(10,0) and the origin be denoted by o(0,0)
We know that
In a right angled triangle the angle oppposite the hypotenuse subtend an angle of 90°
Let us find distance AB, AO, BO
`AB = sqrt((10 - 0)^2 + (0 - 100)^2)`
`= sqrt(100 + 10000)`
`= sqrt(10100)` units
`AO = sqrt((0 - 0)^2 + (0 - 100)^2)`
= `sqrt(100)` untis
Her we can see that, `AO^2 + BO^2 = AB^2`
Therefore, ΔAOB is a right angled triangle with AB being the hypotenuse.
So the angle subtended at the origin by the giving line segment is 90°
APPEARS IN
RELATED QUESTIONS
Find the values of k so that the area of the triangle with vertices (1, -1), (-4, 2k) and (-k, -5) is 24 sq. units.
ΔABC is right angled at A (see the given figure). AD is perpendicular to BC. If AB = 5 cm, BC = 13 cm and AC = 12 cm, Find the area of ΔABC. Also find the length of AD.

The point A divides the join of P (−5, 1) and Q(3, 5) in the ratio k:1. Find the two values of k for which the area of ΔABC where B is (1, 5) and C(7, −2) is equal to 2 units.
In a ΔABC, AB = 15 cm, BC = 13 cm and AC = 14 cm. Find the area of ΔABC and hence its altitude on AC ?
Show that the following points are collinear:
A(5,1), B(1, -1) and C(11, 4)
Show that the points (a + 5, a – 4), (a – 2, a + 3) and (a, a) do not lie on a straight line for any value of a.
Let `Delta = abs (("x", "y", "z"),("x"^2, "y"^2, "z"^2),("x"^3, "y"^3, "z"^3)),` then the value of `Delta` is ____________.
The area of a triangle with vertices (a, b + c), (b, c + a) and (c, a + b) is ______.
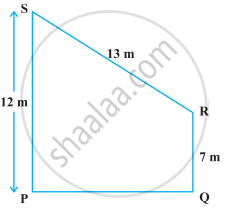
Find the area of the trapezium PQRS with height PQ given in the following figure.
Using determinants, find the area of ΔPQR with vertices P(3, 1), Q(9, 3) and R(5, 7). Also, find the equation of line PQ using determinants.
