Advertisements
Advertisements
Question
Show that the following points are collinear:
A(5,1), B(1, -1) and C(11, 4)
Solution
`"Let" A(x_1=5,y_1=1), B(x_2=1,y_2=-1) and C(x_3=11,y_3=4)`be the given points.
Now `x_1 (y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)`
=5(-1-4)+1(4-1)+11(1+1)
=-25+3+22
=0
Hence, the given points are collinear.
APPEARS IN
RELATED QUESTIONS
Find the values of k so that the area of the triangle with vertices (k + 1, 1), (4, -3) and (7, -k) is 6 sq. units.
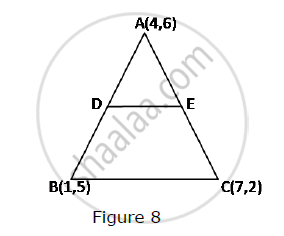
In Fig. 8, the vertices of ΔABC are A(4, 6), B(1, 5) and C(7, 2). A line-segment DE is drawn to intersect the sides AB and AC at D and E respectively such that `(AD)/(AB)=(AE)/(AC)=1/3 `Calculate th area of ADE and compare it with area of ΔABCe.
Find the area of the quadrilateral whose vertices, taken in order, are (-4, -2), (-3, -5), (3, -2) and (2, 3).
ΔABC is isosceles with AB = AC = 7.5 cm and BC = 9 cm (see the given figure). The height AD from A to BC, is 6 cm. Find the area of ΔABC. What will be the height from C to AB i.e., CE?

Find the area of a triangle whose vertices are
(6,3), (-3,5) and (4,2)
Find the centroid of the triangle whosw vertices is (1,4), (-1,1) and (3,2) .
Show that the following points are collinear:
(i) A(2,-2), B(-3, 8) and C(-1, 4)
If the points P(-3, 9), Q(a, b) and R(4, -5) are collinear and a+b=1, find the value of a and b.
What is the area of a triangle with base 4.8 cm and height 3.6 cm?
If the co-ordinates of the vertices of an equilateral triangle with sides of length ‘a’ are (x1, y1), (x2, y2), (x3, y3), then `|(x_1, y_1, 1),(x_2, y_2, 1),(x_3, y_3, 1)|^2 = (3"a"^4)/4`
