Advertisements
Advertisements
Question
Find the values of k so that the area of the triangle with vertices (1, -1), (-4, 2k) and (-k, -5) is 24 sq. units.
Solution
Take (x1,y1)=(1,-1),(4,-2k)and (-k,-5)
It is given that the area of the triangle is 24 sq.unit Area of the triangle having vertices (x1,y1),(x2,y2) and (x3,y3) is given by
`=1/2[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]`
`24=1/2[1(2k-(-5)+(-4)((-5)-(-1))+(-k)((-1)-2k)]`
`48=[(2k+5)+16+(k+2k^2)]`
`2k^2+3k-27=0`
`(2k+9)(k-3)=0`
`k=-9/2 or k=3`
The values of k are -9/2 and 3.
APPEARS IN
RELATED QUESTIONS
Find the area of the following triangle:
Prove that the lines joining the middle points of the opposite sides of a quadrilateral and the join of the middle points of its diagonals meet in a point and bisect one another
Show that the following points are collinear:
A(8,1), B(3, -4) and C(2, -5)
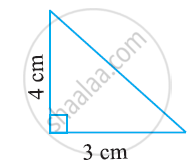
Find the area of the following triangle:

In ∆PQR, PR = 8 cm, QR = 4 cm and PL = 5 cm. 
Find:
(i) the area of the ∆PQR
(ii) QM.
The points (0, 5), (0, –9) and (3, 6) are collinear.
The area of ∆ABC is 8 cm2 in which AB = AC = 4 cm and ∠A = 90º.
The base and the corresponding altitude of a parallelogram are 10 cm and 3.5 cm, respectively. The area of the parallelogram is 30 cm2.
Find the missing value:
| Base | Height | Area of parallelogram |
| ______ | 8.4 cm | 48.72 cm2 |
Ratio of the area of ∆WXY to the area of ∆WZY is 3:4 in the given figure. If the area of ∆WXZ is 56 cm2 and WY = 8 cm, find the lengths of XY and YZ.

