Advertisements
Advertisements
Question
Show that the points (a + 5, a – 4), (a – 2, a + 3) and (a, a) do not lie on a straight line for any value of a.
Solution
Given, the points are (a + 5, a – 4), (a – 2, a + 3) and (a, a).
We have to prove that these pints do not lie on a straaighine.
So, we have to prove that these points form a triangle.
Area, Δ = `1/2|("a" + 5, "a" - 4, 1),("a" - 2, "a" + 3, 1),("a", "a", 1)|`
[Applying R1 → R1 – R3 and R2 → R2 – R3]
= `1/2 |(5, -4, 0),(-2, 3, 0),("a", "a", 1)|`
= `1/2[(1 * (15 - 8)]`
= `7/2 ≠ 0`
Hence, given points from a triangle i.e., points do not lie on a straight line.
APPEARS IN
RELATED QUESTIONS
Find the relation between x and y if, the points A(x, y), B(-5, 7) and C(-4, 5) are collinear.
A(4, - 6), B(3,- 2) and C(5, 2) are the vertices of a 8 ABC and AD is its median. Prove that the median AD divides Δ ABC into two triangles of equal areas.
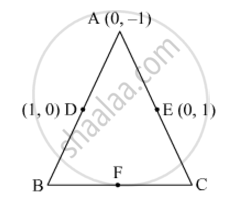
In Fig. 6, ABC is a triangle coordinates of whose vertex A are (0, −1). D and E respectively are the mid-points of the sides AB and AC and their coordinates are (1, 0) and (0, 1) respectively. If F is the mid-point of BC, find the areas of ∆ABC and ∆DEF.
If the points A(−2, 1), B(a, b) and C(4, −1) are collinear and a − b = 1, find the values of a and b.
If A(−4, 8), B(−3, −4), C(0, −5) and D(5, 6) are the vertices of a quadrilateral ABCD, find its area.
Find the area of the triangle PQR with Q(3,2) and the mid-points of the sides through Q being (2,−1) and (1,2).
The vertices of ∆ABC = are A (4, 6), B(1, 5) and C(7, 2). A line is drawn to intersect sides AB and AC at D and E respectively such that `\frac{AD}{AB}=\frac{AE}{AC}=\frac{1}{4}` .Calculate the area of ∆ADE and compare it with the area of ∆ABC
If the coordinates of two points A and B are (3, 4) and (5, – 2) respectively. Find the coordniates of any point P, if PA = PB and Area of ∆PAB = 10
Find the area of a triangle with vertices at the point given in the following:
(2, 7), (1, 1), (10, 8)
The area of a triangle is 5 sq units. Two of its vertices are (2, 1) and (3, –2). If the third vertex is (`7/2`, y). Find the value of y
If A(–5, 7), B(–4, –5), C(–1, –6) and D(4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD
Show that the following sets of points are collinear.
(2, 5), (4, 6) and (8, 8)
Show that the following sets of points are collinear.
(1, −1), (2, 1) and (4, 5)
Prove that the points (a, 0), (0, b) and (1, 1) are collinear if `1/a+1/b=1`
Find the area of a triangle whose sides are respectively 150 cm, 120 cm and 200 cm ?
Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42cm ?
Show that the points O(0,0), A`( 3,sqrt(3)) and B (3,-sqrt(3))` are the vertices of an equilateral triangle. Find the area of this triangle.
A(6,1) , B(8,2) and C(9,4) are the vertices of a parallelogram ABCD. If E is the midpoint of DC, find the area of ΔADE
Show that the following points are collinear:
(i) A(2,-2), B(-3, 8) and C(-1, 4)
Find the area of ΔABC with vertices A(0, -1), B(2,1) and C(0, 3). Also, find the area of the triangle formed by joining the midpoints of its sides. Show that the ratio of the areas of two triangles is 4:1.
Find the value(s) of p for which the points (3p + 1, p), (p + 2, p – 5) and (p + 1, –p) are collinear ?
Find the area of the following triangle:

A field is in the shape of a right angled triangle whose base is 25 m and height 20 m. Find the cost of levelling the field at the rate of ₹ 45 per sq.m2
If A, B, C are the angles of a triangle, then ∆ = `|(sin^2"A", cot"A", 1),(sin^2"B", cot"B", 1),(sin^2"C", cot"C", 1)|` = ______.
The area of a triangle with vertices A(3, 0), B(7, 0) and C(8, 4) is ______.
Points A(–6, 10), B(–4, 6) and C(3, –8) are collinear such that AB = `2/9` AC.
The area of ∆ABC is 8 cm2 in which AB = AC = 4 cm and ∠A = 90º.
In the given figure, ΔMNO is a right-angled triangle. Its legs are 6 cm and 8 cm long. Length of perpendicular NP on the side MO is ______.

In the given figure, area of ΔPQR is 20 cm2 and area of ΔPQS is 44 cm2. Find the length RS, if PQ is perpendicular to QS and QR is 5 cm.

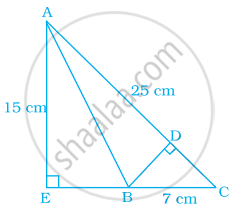
In the given figure, triangle AEC is right-angled at E, B is a point on EC, BD is the altitude of triangle ABC, AC = 25 cm, BC = 7 cm and AE = 15 cm. Find the area of triangle ABC and the length of DB.