Advertisements
Advertisements
Question
A(4, - 6), B(3,- 2) and C(5, 2) are the vertices of a 8 ABC and AD is its median. Prove that the median AD divides Δ ABC into two triangles of equal areas.
Solution
Solution:
Let the co-ordinates of D be D (x,y) and D is midpoint of BC
x = (3+5)/2 = 4; y = (2-2)/2 = 0
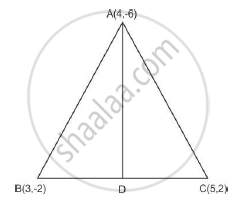
Now Area of triangle ABD = `1/2 [4(-2-0) +3(0+6)+4(-6+2)]` = `3 `
and Area of triangle ACD `=1/2 [5(-6-0) + 4(0 - 2) + 4(2+6)] = 3 `
Hence, the median AD divides triangle ABC into two triangle of equal area.
APPEARS IN
RELATED QUESTIONS
The area of a triangle is 5 sq units. Two of its vertices are (2, 1) and (3, –2). If the third vertex is (`7/2`, y). Find the value of y
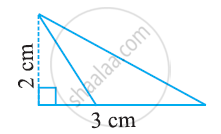
Find the area of the following triangle:
Prove that the points (a, 0), (0, b) and (1, 1) are collinear if `1/a+1/b=1`
Prove that the lines joining the middle points of the opposite sides of a quadrilateral and the join of the middle points of its diagonals meet in a point and bisect one another
Using determinants, find the values of k, if the area of triangle with vertices (–2, 0), (0, 4) and (0, k) is 4 square units.
Using integration, find the area of triangle ABC, whose vertices are A(2, 5), B(4, 7) and C(6, 2).
What is the area of a triangle with base 4.8 cm and height 3.6 cm?
Find BC, if the area of the triangle ABC is 36 cm2 and the height AD is 3 cm.

If A, B, C are the angles of a triangle, then ∆ = `|(sin^2"A", cot"A", 1),(sin^2"B", cot"B", 1),(sin^2"C", cot"C", 1)|` = ______.
Points A(3, 1), B(12, –2) and C(0, 2) cannot be the vertices of a triangle.
