Advertisements
Advertisements
Question
Show that the following sets of points are collinear.
(1, −1), (2, 1) and (4, 5)
Solution
The formula for the area ‘A’ encompassed by three points, (x1,y1) (x2,y2)and (x3,y3) is given by the formula,
We know area o triangle formed by three points (x1,y1),(x2,y2),(x3,y3) is given by
`Δ=1/2[x_1(y_2-y_3)+x_2 (y_3-y_1)+x_3(y_1-y_2)] `
The three given points are A(1, −1), B(2, 1) and C(4, 5). Substituting these values in the earlier mentioned formula we have,
A`=1/2[1(1-5)+2(5+1)+4(-1-1)]`
`=1/2[1(-4)+2(6)+4(-2)]`
`=1/2[-4+12+8]`
`=1/2[-12+12]`
`=0`
Since the area enclosed by the three points is equal to 0, the three points need to be collinear.
APPEARS IN
RELATED QUESTIONS
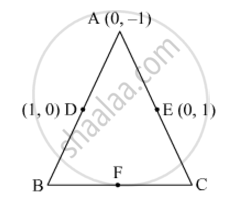
In Fig. 6, ABC is a triangle coordinates of whose vertex A are (0, −1). D and E respectively are the mid-points of the sides AB and AC and their coordinates are (1, 0) and (0, 1) respectively. If F is the mid-point of BC, find the areas of ∆ABC and ∆DEF.
If the coordinates of two points A and B are (3, 4) and (5, – 2) respectively. Find the coordniates of any point P, if PA = PB and Area of ∆PAB = 10
For what value of a point (a, 1), (1, -1) and (11, 4) are collinear?
Find the value(s) of p for which the points (3p + 1, p), (p + 2, p – 5) and (p + 1, –p) are collinear ?
If the points A (x, y), B (3, 6) and C (−3, 4) are collinear, show that x − 3y + 15 = 0.
In ☐ABCD, l(AB) = 13 cm, l(DC) = 9 cm, l(AD) = 8 cm, find the area of ☐ABCD.

If A, B, C are the angles of a triangle, then ∆ = `|(sin^2"A", cot"A", 1),(sin^2"B", cot"B", 1),(sin^2"C", cot"C", 1)|` = ______.
Find the area of the triangle whose vertices are (-2, 6), (3, -6), and (1, 5).
The points (1,1), (-2, 7) and (3, -3) are ______.
Observe all the four triangles FAB, EAB, DAB and CAB as shown in the given figure.

- All triangles have the same base and the same altitude.
- All triangles are congruent.
- All triangles are equal in area.
- All triangles may not have the same perimeter.
