Advertisements
Advertisements
Question
Find the value(s) of p for which the points (3p + 1, p), (p + 2, p – 5) and (p + 1, –p) are collinear ?
Solution
Since the given points are collinear, the area of the triangle formed by them must be 0.
\[ \Rightarrow 4 p^2 - 12p = 0\]
\[ \Rightarrow p\left( 4p - 12 \right) = 0\]
\[ \Rightarrow p = 0\ \text{or}\ 4p - 12 = 0\]
\[ \Rightarrow p = 0\ \text{or}\ p = 3\]
APPEARS IN
RELATED QUESTIONS
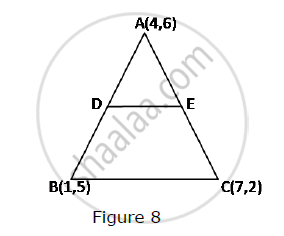
In Fig. 8, the vertices of ΔABC are A(4, 6), B(1, 5) and C(7, 2). A line-segment DE is drawn to intersect the sides AB and AC at D and E respectively such that `(AD)/(AB)=(AE)/(AC)=1/3 `Calculate th area of ADE and compare it with area of ΔABCe.
If A(4, –6), B(3, –2) and C(5, 2) are the vertices of ∆ABC, then verify the fact that a median of a triangle ABC divides it into two triangle of equal areas.
Find the area of the following triangle:

prove that the points A (7, 10), B(-2, 5) and C(3, -4) are the vertices of an isosceles right triangle.
Show that the points A(-5,6), B(3,0) and C(9,8) are the vertices of an isosceles right-angled triangle. Calculate its area.
Find the value of x for which points A(x, 2), B(-3, -4) and C(7, -5) are collinear.
If the points A(1, 2), O(0, 0) and C(a, b) are collinear, then ______.
The dimensions of a rectangle ABCD are 51 cm × 25 cm. A trapezium PQCD with its parallel sides QC and PD in the ratio 9 : 8, is cut off from the rectangle as shown in the following figure. If the area of the trapezium PQCD is `5/6` th part of the area of the rectangle, find the lengths QC and PD.

Ratio of the area of ∆WXY to the area of ∆WZY is 3:4 in the given figure. If the area of ∆WXZ is 56 cm2 and WY = 8 cm, find the lengths of XY and YZ.

Find the missing value:
| Base | Height | Area of Triangle |
| 22 cm | ______ | 170.5 cm2 |
