Advertisements
Advertisements
Questions
The angle of elevation of the top of a chimney form the foot of a tower is 60° and the angle of depression of the foot of the chimney from the top of the tower is 30° . If the height of the tower is 40 meters. Find the height of the chimney.
The angle of elevation of the top of a chimney from the foot of a tower is 60° and the angle of depression of the foot of the chimney from the top of the tower is 30°. If the height of the tower is 40 m, find the height of the chimney. According to pollution control norms, the minimum height of a smoke emitting chimney should be 100 m. State if the height of the above mentioned chimney meets the pollution norms. What value is discussed in this question?
Solution
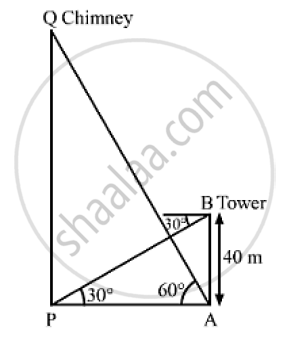
Let PQ be the chimney and AB be the tower.
We have,
AB = 40m,∠APB = 30° and ∠PAQ = 60°
In ΔABP,
`tan 30° = (AB)/(AP)`
`⇒ 1/ sqrt(3) = 40/ (AP)`
`⇒ AP = 40 sqrt(3 ) m`
Now, in Δ APQ ,
` tan 60° = (OQ)/(AP)`
`⇒ sqrt(3) = (PQ) / (40 sqrt(3))`
∴ PQ = 120 m
So, the height of the chimney is 120 m.
Hence, the height of the chimney meets the pollution norms.
In this question, management of air pollution has been shown
RELATED QUESTIONS
A person standing on the bank of river observes that the angle of elevation of the top of a tree standing on the opposite bank is 60°. When he moves 40 m away from the bank, he finds the angle of elevation to be 30°. Find the height of the tree and width of the river. `(sqrt 3=1.73)`
The altitude of the sun at any instant is 60º. Find the height of the vertical pole that will cast a shadow of 30 m.
From the top of a 15 m high building, the angle of elevation of the top of a tower is found to be 30°. From the bottom of the same building, the angle of elevation of the top of the tower is found to be 60°. Find the height of the tower and the distance between tower and the building.
If the angles of elevation of the top of a tower from two points distant a and b from the base and in the same straight line with it are complementary, then the height of the tower is
From a light house the angles of depression of two ships on opposite sides of the light house are observed to be 30° and 45°. If the height of the light house is h metres, the distance between the ships is
Two buildings are in front of each other on either side of a road of width 10 metres. From the top of the first building which is 20 metres high, the angle of elevation to the top of the second is 45°. What is the height of the second building?
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the height of the lamp post
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the difference between height of the lamp post and the apartment
A plane is observed to be approaching the airport. It is at a distance of 12 km from the point of observation and makes an angle of elevation of 60°. The height above the ground of the plane is ____________.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
