Advertisements
Advertisements
Question
The horizontal distance between two towers is 60 meters. The angle of depression of the top of the first tower when seen from the top of the second tower is 30° . If the height of the second tower is 90 meters. Find the height of the first tower.
Solution
Let DE be the first tower and AB be the second tower.
Now, AB = 90 m and AD = 60 m such that CE = 60 m and ∠BEC = 30°.
Let DE = h m such that AC = h m and BC = (90- h)m.
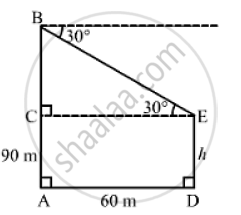
In the right ΔBCE,we have:
`(BC)/(CE) = tan 30° = 1/ sqrt(3)`
`⇒ ((90-h )) /60 = 1/ sqrt(3) `
`⇒ (90-h ) sqrt(3) = 60`
`⇒ h sqrt(3) = 90 sqrt( 3 ) -60`
`⇒ h = 90- 60/ sqrt(3) = 90- 34.64 = 55.36 m`
∴ Height of the first tower = DE = h = 55.36m
APPEARS IN
RELATED QUESTIONS
A 1.6 m tall girl stands at a distance of 3.2 m from a lamp-post and casts a shadow of 4.8 m on the ground. Find the height of the lamp-post by using (i) trigonometric ratios (ii) property of similar triangles.
The angles of depression of the top and bottom of a tower as seen from the top of a 60 `sqrt(3)` m high cliff are 45° and 60° respectively. Find the height of the tower.
A ladder 15 m long makes an angle of 60° with the wall. Find the height of the point where the ladder touches the wall.
The angle of depression of a car, standing on the ground, from the top of a 75 m high tower, is 30°. The distance of the car from the base of the tower (in m.) is:
An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top of the tower from the eye of the observer.
A road is flanked on either side by continuous rows of houses of height `4sqrt(3)` m with no space in between them. A pedestrian is standing on the median of the road facing a row house. The angle of elevation from the pedestrian to the top of the house is 30°. Find the width of the road
The angle of elevation of the top of a tower from two points distant s and t from its foot are complementary. Prove that the height of the tower is `sqrt(st)`
From the top of a tower h m high, the angles of depression of two objects, which are in line with the foot of the tower are α and β (β > α). Find the distance between the two objects.
A boy 1.7 m tall is standing on a horizontal ground, 50 m away from a building. The angle of elevation of the top of the building from his eye is 60°. Calculate the height of the building. (Take `sqrt(3)` = 1.73)
An aeroplane when flying at a height of 3125 m from the ground passes vertically below another plane at an instant when the angles of elevation of the two planes from the same point on the ground are 30° and 60° respectively. Find the distance between the two planes at that instant.
