Advertisements
Advertisements
प्रश्न
The horizontal distance between two towers is 60 meters. The angle of depression of the top of the first tower when seen from the top of the second tower is 30° . If the height of the second tower is 90 meters. Find the height of the first tower.
उत्तर
Let DE be the first tower and AB be the second tower.
Now, AB = 90 m and AD = 60 m such that CE = 60 m and ∠BEC = 30°.
Let DE = h m such that AC = h m and BC = (90- h)m.
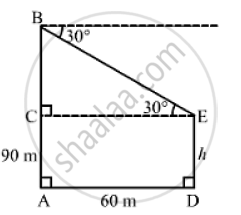
In the right ΔBCE,we have:
`(BC)/(CE) = tan 30° = 1/ sqrt(3)`
`⇒ ((90-h )) /60 = 1/ sqrt(3) `
`⇒ (90-h ) sqrt(3) = 60`
`⇒ h sqrt(3) = 90 sqrt( 3 ) -60`
`⇒ h = 90- 60/ sqrt(3) = 90- 34.64 = 55.36 m`
∴ Height of the first tower = DE = h = 55.36m
APPEARS IN
संबंधित प्रश्न
The pilot of a helicopter, at an altitude of 1200m finds that the two ships are sailing towards it in the same direction. The angle of depression of the ships as observed from the helicopter are 60º and 45º respectively. Find the distance between the two ships
From the top of a tower, 100, high, a man observes two cars on the opposite sides of the tower and in same straight line with its base, with angles of depression 30° and 45°. Find the distance between the cars. [Take `sqrt3` = 1.732]
The length of a string between a kite and a point on the ground is 90 meters. If the string makes an angle O with the ground level such that tan O = 15/8, how high is the kite? Assume that there is no slack in the string.
A statue 1.46m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the status is 60 and from the same point, the angle of elevation of the top of the pedestal is 45 . Find the height of the pedestal.
If the height of a vertical pole is 3–√3 times the length of its shadow on the ground, then the angle of elevation of the Sun at that time is
(A) 30°
(B) 60°
(C) 45°
(D) 75°
Two ships are approaching a light-house from opposite directions. The angles of depression of the two ships from the top of the light-house are 30° and 45°. If the distance between the two ships is 100 m, find the height of the light-house. \[[Use \sqrt{3} = 1 . 732]\]
From the top of the light house, an observer looks at a ship and finds the angle of depression to be 30°. If the height of the light-house is 100 meters, then find how far the ship is from the light-house.
The angle of elevation of the top of a cell phone tower from the foot of a high apartment is 60° and the angle of depression of the foot of the tower from the top of the apartment is 30°. If the height of the apartment is 50 m, find the height of the cell phone tower. According to radiation control norms, the minimum height of a cell phone tower should be 120 m. State if the height of the above mentioned cell phone tower meets the radiation norms
If a man standing on a platform 3 metres above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.
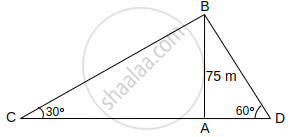
Two men on either side of a cliff 75 m high observe the angles of elevation of the top of the cliff to be 30° and 60°. Find the distance between the two men.