Question

If a man standing on a platform 3 metres above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.

पर्याय

• True

• False

Answer 1

This statement is False.

Explanation:

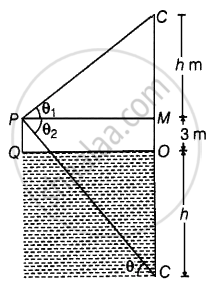
From figure, we observe that, a man standing on a platform at point P, 3 m above the surface of a lake observes a cloud at point C.

Let the height of the cloud from the surface of the platform is h and angle of elevation of the cloud is θ₁.

Now at same point P a man observes a cloud reflection in the lake at this time the height of reflection of cloud in lake is (h + 3) because in lake platform height is also added to reflection of cloud.

So, angle of depression is different in the lake from the angle of elevation of the cloud above the surface of a lake

In ΔMPC,

tan θ₁ = `"CM"/"PM" = "h"/"PM"`

⇒ `(tan θ_1)/"h" = 1/"PM"`  ...(i)

In ΔCPM,

tan θ₂ = `"CM"/"PM"`

= `("OC" + "OM")/"PM"`

= `("h" + 3)/"PM"`

⇒ `(tan θ_2)/("h" + 3) = 1/"PM"`   ...(ii)

From equations (i) and (ii),

`(tan θ_1)/"h" = (tan θ_2)/("h" + 3)`

⇒ tan θ₂ = `(("h" + 3)/"h") tan θ_1`

Hence, θ₁ ≠ θ₂