Advertisements
Advertisements
प्रश्न
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun is also increasing.
पर्याय
True
False
उत्तर
This statement is False.
Explanation:
To understand the fact of this question, consider the following example
I. A tower `2sqrt(3)` m high casts a shadow 2 m long on the ground, then the Sun’s elevation is 60°.
In ΔACB,
tan θ = `"AB"/"BC" = (2sqrt(3))/2`
⇒ tan θ = `sqrt(3)` = tan 60°
∴ θ = 60°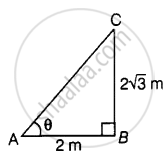
II. A same height of tower casts a shadow 4m more from preceding point, then the Sun’s elevation is 30°.
In ΔAPB,
tan θ = `"AB"/"PB" = "AB"/("PC" + "CB")`
⇒ tan θ = `(2sqrt(3))/(4 + 2) = (2sqrt(3))/6`
⇒ tan θ = `sqrt(3)/3 * sqrt(3)/sqrt(3) = 3/(3sqrt(3)`
⇒ tan θ = `1/sqrt(3)` = tan 30°
∴ θ = 30°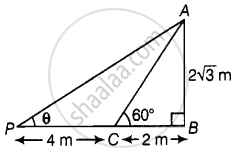
Hence, we conclude from above two examples that if the length of the shadow of a tower is increasing, then the angle of elevation of the Sun is decreasing.
APPEARS IN
संबंधित प्रश्न
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 45°. If the tower is 30 m high, find the height of the building.
A storm broke a tree and the treetop rested 20 m from the base of the tree, making an angle of 60° with the horizontal. Find the height of the tree.
If the angles of elevation of the top of a tower from two points distant a and b from the base and in the same straight line with it are complementary, then the height of the tower is
A building and a statue are in opposite side of a street from each other 35 m apart. From a point on the roof of building the angle of elevation of the top of statue is 24° and the angle of depression of base of the statue is 34°. Find the height of the statue. (tan 24° = 0.4452, tan 34° = 0.6745)
A window of a house is h meters above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be A and B respectively. Then the height of the other house is ____________.
The angle of elevation of the top of a tower from certain point is 30°. If the observer moves 20 metres towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower.
If a man standing on a platform 3 metres above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.
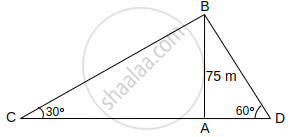
Two men on either side of a cliff 75 m high observe the angles of elevation of the top of the cliff to be 30° and 60°. Find the distance between the two men.
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45°. If the bridge is at a height of 8 m from the banks, then find the width of the river.
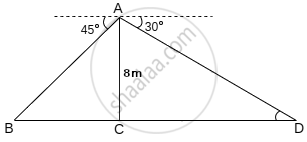
Read the following passage and answer the questions given below.
|
Qutub Minar, located in South Delhi, India was built in the year 1193. It is 72 m high tower. Working on a school project, Charu and Daljeet visited the monument. They used trigonometry to find their distance from the tower. Observe the picture given below. Points C and D represent their positions on the ground in line with the base of tower, the angles of elevation of top of the tower (Point A) are 60° and 45° from points C and D respectively.
|
- Based on the above information, draw a well-labelled diagram.
- Find the distances CD, BC and BD. [use `sqrt(3)` = 1.73]

