Advertisements
Advertisements
प्रश्न
A building and a statue are in opposite side of a street from each other 35 m apart. From a point on the roof of building the angle of elevation of the top of statue is 24° and the angle of depression of base of the statue is 34°. Find the height of the statue. (tan 24° = 0.4452, tan 34° = 0.6745)
उत्तर
Let the height of the statue be h m
Let AD be x
∴ EC = h – x
In the right ∆ABD,
tan 34° = `"AD"/"AB"`
0.6745 = `x/35`
∴ x = 0.6745 × 35
⇒ x = 23.61 m
In the right ∆DEC
⇒ tan 24° = `"EC"/"DE"`
0.4452 = `("h" - x)/35`
⇒ h – x = 0.4452 × 35
h – 23.61 = 15.58
⇒ h = 15.58 + 23.61
= 39.19 m
Height of the statue = 39.19 m
APPEARS IN
संबंधित प्रश्न
The angle of elevation of the top of a vertical tower from a point on the ground is 60° . From another point 10 m vertically above the first, its angle of elevation is 30° .Find the height of the tower.
From the top of a vertical tower, the angles depression of two cars in the same straight line with the base of the tower, at an instant are found to be 45° and 60° . If the cars are 100 m apart and are on the same side of the tower, find the height of the tower.
A pole casts a shadow of length \[2\sqrt{3}\] m on the ground, when the sun's elevation is 60°. Find the height of the pole.
From the top of a tower of height 50 m, the angles of depression of the top and bottom of a pole are 30° and 45° respectively. Find
(i) how far the pole is from the bottom of a tower,
(ii) the height of the pole. (Use \[\sqrt{3} = 1 . 732\])
A tower stands vertically on the ground. From a point on the ground which is 25 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 45°. Then the height (in meters) of the tower is
It is found that on walking x meters towards a chimney in a horizontal line through its base, the elevation of its top changes from 30° to 60°. The height of the chimney is
Find the positive value of m for which the distance between the points A(5, −3) and B(13, m) is 10 units.
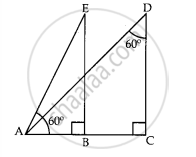
In given Fig., the angle of depression from the observing position D and E of the object at A are ____________.
A portion of a 60 m long tree is broken by a tornado and the top struck up the ground making an angle of 30° with the ground level. The height of the point where the tree is broken is equal to ____________.
Two vertical poles AB = 15 m and CD = 10 m are standing apart on a horizontal ground with points A and C on the ground. If P is the point of intersection of BC and AD, then the height of P (in m) above the line AC is ______.
