Advertisements
Advertisements
प्रश्न
From the top of a vertical tower, the angles depression of two cars in the same straight line with the base of the tower, at an instant are found to be 45° and 60° . If the cars are 100 m apart and are on the same side of the tower, find the height of the tower.
उत्तर
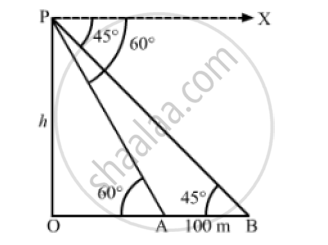
Let OP be the tower and points A and B be the positions of the cars.
We have,
AB =100m, ∠OAP = 60° and ∠OBP = 45°
Let OP = h
In ΔAOP,
` tan 60° = (OP)/(OA)`
`⇒ sqrt(3) = h/(OA)`
`⇒OA = h/sqrt(3)`
Also, in Δ BOP ,
` tan 45° = (OP)/(OB)`
`⇒ 1 = h/(OB)`
⇒ OB = h
Now,OB - OA = 100
`⇒ h - h/sqrt(3) = 100`
` ⇒ (h sqrt(3)-h)/sqrt(3) = 100`
`⇒(h(sqrt(3) -h))/sqrt(3) = 100`
`h = (100sqrt(3) )/((sqrt(3)-1)) xx ((sqrt(3)+1))/((sqrt(3)+1))`
`h = (100 sqrt(3) ( sqrt(3)+1))/((3-1))`
`⇒ h = (100(3+sqrt(3)))/2`
⇒ h = 50(3+1.732)
⇒ h =50(4.732)
∴ h =236.6m
So, the height of the tower is 236.6 m.
Disclaimer. The answer given in the textbook is incorrect. The same has been rectified above.
संबंधित प्रश्न
There is a small island in the middle of a 100 m wide river and a tall tree stands on the island. P and Q are points directly opposite to each other on two banks, and in line with the tree. If the angles of elevation of the top of the tree from P and Q are respectively 30º and 45º, find the height of the tree. (Use `sqrt(3)` = 1.732)
A tower stands vertically on the ground. From a point on the ground, 20 m away from the foot of the tower, the angle of elevation of the top of the tower is 600. What is the height of the tower?
A kit is flying at a height of 75 metres from the ground level, attached to a string inclined at 60 to the horizontal. Find the length of the string to the nearest metre.
A pole casts a shadow of length \[2\sqrt{3}\] m on the ground, when the sun's elevation is 60°. Find the height of the pole.
The angle of elevation of the top of a cell phone tower from the foot of a high apartment is 60° and the angle of depression of the foot of the tower from the top of the apartment is 30°. If the height of the apartment is 50 m, find the height of the cell phone tower. According to radiation control norms, the minimum height of a cell phone tower should be 120 m. State if the height of the above mentioned cell phone tower meets the radiation norms
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is B to the North of A?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is C to the East of B?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
If at some time, the length of the shadow of a tower is `sqrt3` times its height, then the angle of elevation of the sun, at that time is ____________.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
From the top of a tower h m high, the angles of depression of two objects, which are in line with the foot of the tower are α and β (β > α). Find the distance between the two objects.
