Advertisements
Advertisements
Question
From the top of a vertical tower, the angles depression of two cars in the same straight line with the base of the tower, at an instant are found to be 45° and 60° . If the cars are 100 m apart and are on the same side of the tower, find the height of the tower.
Solution
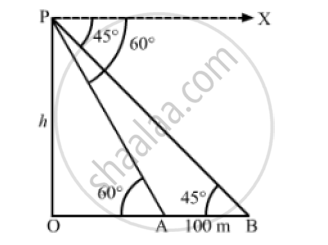
Let OP be the tower and points A and B be the positions of the cars.
We have,
AB =100m, ∠OAP = 60° and ∠OBP = 45°
Let OP = h
In ΔAOP,
` tan 60° = (OP)/(OA)`
`⇒ sqrt(3) = h/(OA)`
`⇒OA = h/sqrt(3)`
Also, in Δ BOP ,
` tan 45° = (OP)/(OB)`
`⇒ 1 = h/(OB)`
⇒ OB = h
Now,OB - OA = 100
`⇒ h - h/sqrt(3) = 100`
` ⇒ (h sqrt(3)-h)/sqrt(3) = 100`
`⇒(h(sqrt(3) -h))/sqrt(3) = 100`
`h = (100sqrt(3) )/((sqrt(3)-1)) xx ((sqrt(3)+1))/((sqrt(3)+1))`
`h = (100 sqrt(3) ( sqrt(3)+1))/((3-1))`
`⇒ h = (100(3+sqrt(3)))/2`
⇒ h = 50(3+1.732)
⇒ h =50(4.732)
∴ h =236.6m
So, the height of the tower is 236.6 m.
Disclaimer. The answer given in the textbook is incorrect. The same has been rectified above.
RELATED QUESTIONS
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
The shadow of a tower, when the angle of elevation of the sun is 45°, is found to be 10 m. longer than when it was 600. Find the height of the tower.
The shadow of a tower standing on a level ground is found to be 40 m longer when Sun’s altitude is 30° than when it was 60°. Find the height of the tower.
The vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height 6m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is
30 and that of the top of the flagstaff 60 . Find the height of the tower
[Use `sqrt(3)` 1.732 ]
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60° . At a point Y, 40m vertically above X, the angle of elevation is 45° . Find the height of tower PQ.
An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top of the tower from the eye of the observer.
The height of a tower is 100 m. When the angle of elevation of the sun changes from 30° to 45°, the shadow of the tower becomes x metres less. The value of x is
The angle of depression of the top and bottom of 20 m tall building from the top of a multistoried building are 30° and 60° respectively. The height of the multistoried building and the distance between two buildings (in metres) is
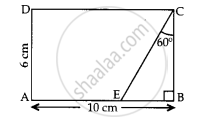
In given figure, the value of CE is ____________.
The angle of elevation of the top of a tower from a certain point is 30°. If the observer moves 20 meters towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower ____________.
