Advertisements
Advertisements
Question
A ladder of length 6meters makes an angle of 45° with the floor while leaning against one wall of a room. If the fort of the ladder is kept fixed on the floor and it is made to lean against the opposite wall of the room, it makes an angle of 60° with the floor. Find the
distance between two walls of the room.
Solution
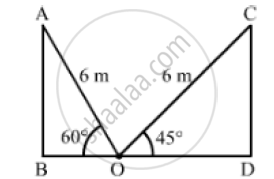
Let AB and CD be the two opposite walls of the room and the foot of the ladder be fixed at
the point O on the ground.
We have,
AO = CO = 6m,∠AOB = 60° and ∠COD = 45°
In ΔABO,
`cos 60°= (BD)/(AO)`
`⇒1/2 = (BO)/6`
`⇒ BO = 6/2`
⇒ BO = 3m
Also, in ΔCDO,
`cos 45° = (DO)/(CO)`
`⇒1/sqrt(2) = (DO)/6`
`⇒ DO = 6/sqrt(2) xx sqrt(2)/sqrt(2)`
`⇒DO = (6 sqrt(2))/2`
`⇒ Do = 3 sqrt(2) m`
Now, the distance between two walls of the room = BD
=BO+DO
`=3+3sqrt(2) `
`=3(1+sqrt(2))`
=3(1+1.414)
=3(2.414)
=7.242
`~~7.24m`
So, the distant between two walls of the room is 7. 24 m.
APPEARS IN
RELATED QUESTIONS
The angle of elevation of the top of a tower from a point A due south of the tower is α and from B due east of the tower is β. If AB = d, show that the height of the tower is
`\frac{d}{\sqrt{\cot ^{2}\alpha +\cot^{2}\beta `
A man observes a car from the top of a tower, which is moving towards the tower with a uniform speed. If the angle of depression of the car changes from 30° to 45° in 12 minutes, find the time taken by the car now to reach the tower.
A kit is flying at a height of 75 metres from the ground level, attached to a string inclined at 60 to the horizontal. Find the length of the string to the nearest metre.
On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 150 m, find the distance between the objects.
A balloon is connected to a meteorological ground station by a cable of length 215 m inclined at 600 to the horizontal. Determine the height of the balloon from the ground. Assume that there is no slack in the cable.
From the top of the tower h metre high , the angles of depression of two objects , which are in the line with the foot of the tower are ∝ and ß (ß> ∝ ) cts .
If the angles of elevation of the top of a tower from two points distant a and b from the base and in the same straight line with it are complementary, then the height of the tower is
The length of the shadow of a tower standing on level ground is found to be 2x metres longer when the sun's elevation is 30°than when it was 45°. The height of the tower in metres is
The angle of depression of a car parked on the road from the top of a 150 m high tower is 30º. The distance of the car from the tower (in metres) is
The angle of elevation of the top P of a vertical tower PQ of height 10 from a point A on the horizontal ground is 45°. Let R be a point on AQ and from a point B, vertically above R, the angle of elevation of P is 60°. If ∠BAQ = 30°, AB = d and the area of the trapezium PQRB is α, then the ordered pair (d, α) is ______.
