Advertisements
Advertisements
Question
A man observes a car from the top of a tower, which is moving towards the tower with a uniform speed. If the angle of depression of the car changes from 30° to 45° in 12 minutes, find the time taken by the car now to reach the tower.
Solution
Suppose AB be the tower of height h meters. Let C be the initial position of the car and let after 12 minutes the car be at D. It is given that the angles of depression at C and D are 30º and 45º respectively.
Let the speed of the car be v meter per minute. Then,
CD = distance travelled by the car in 12 minutes
CD = 12v meters
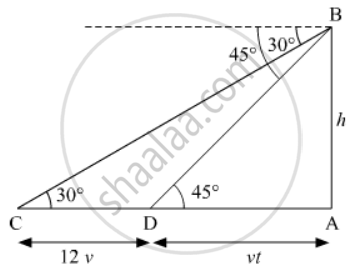
Suppose the car takes t minutes to reach the tower AB from D. Then DA = vt meters
In ∆DAB, we have
`tan 45^@ = (AB)/(AD)`
`=> 1= h/(vt)`.....(i)
In ∆CAB, we have
`tan 30^@ = (AB)/(AB)`
`=> 1/sqrt3 = h/(vt + 12v)`
`=> sqrt3t = vt + 12v` .....(ii)
Substituting the value of h from equation (i) in equation (ii), we get
`=> sqrt3t = t + 12`
`=> t = 12/(sqrt3 - 1) = 12/((sqrt3 - 1)) xx ((sqrt3 + 1))/((sqrt3 + 1)) = 6(sqrt3 + 1)`
t = 16.39 minutes
t = 16 minutes 23 seconds
APPEARS IN
RELATED QUESTIONS
There is a small island in the middle of a 100 m wide river and a tall tree stands on the island. P and Q are points directly opposite to each other on two banks, and in line with the tree. If the angles of elevation of the top of the tree from P and Q are respectively 30º and 45º, find the height of the tree. (Use `sqrt(3)` = 1.732)
The angle of elevation of a cliff from a fixed point is θ. After going up a distance of k metres towards the top of cliff at an angle of φ, it is found that the angle of elevation is α. Show that the height of the cliff is metres
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
The angle of elevation of the top of a tower as observed form a point in a horizontal plane through the foot of the tower is 32°. When the observer moves towards the tower a distance of 100 m, he finds the angle of elevation of the top to be 63°. Find the height of the tower and the distance of the first position from the tower. [Take tan 32° = 0.6248 and tan 63° = 1.9626]
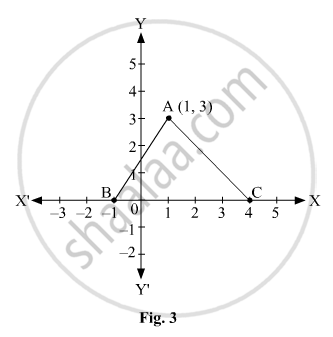
In Fig. 3, the area of triangle ABC (in sq. units) is:
The top of a 15 m high tower makes an angle of elevation of 60° with the bottom of an electronic pole and angle of elevation of 30° with the top of the pole. What is the height of the electric pole?
The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will ____________.
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60° and the angle of elevation of the top of the second tower from the foot of the first tower is 30°. Find the distance between the two towers and also the height of the other tower.
A window of a house is h metres above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be α and β, respectively. Prove that the height of the other house is h(1+ tan α tan β) metres.
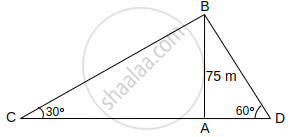
Two men on either side of a cliff 75 m high observe the angles of elevation of the top of the cliff to be 30° and 60°. Find the distance between the two men.