Advertisements
Advertisements
Question
In the given figure, ∆ ABC is a right-angled triangle in which ∠ A is 90°. Semicircles are drawn on AB, AC and BC as diameters. Find the area of the shaded region
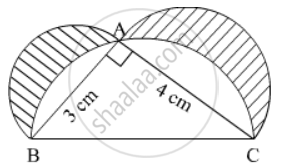
Solution
In right angled ΔABC
`AB^2 + AC^2 = BC^2`
`=> BC = sqrt(AB^2 + AC^2)= sqrt(3^2 + 4^2)`
`=> BC = sqrt(9 + 16) = sqrt25 = 5 cm`
Area of shaded region = {ar (ΔABC) + ar(semicircle on side AB) + ar(semicircle on side AC) } - ar(semicircle on side BC)
Area of shaded region = `[(1/2 xx 3 xx 4)+(1/2pi xx (3/2)^2) +(1/2pi xx (2)^2)] - (1/2pi xx (5/2)^2) cm^2`
`= 6 + 1/2pi(9/4 + 4 - 25/4) cm^2`
= 6 cm2
Hence, area of shaded region is 6 cm2
APPEARS IN
RELATED QUESTIONS
The perimeter of a sector of a circle of radius 5.2 cm is 16.4 cm. Find the area of the sector.
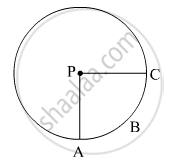
In the given figure, if A(P-ABC) = 154 cm2 radius of the circle is 14 cm, find
(1) `∠APC`
(2) l ( arc ABC) .
The wheel of a motor cycle is of radius 35 cm. How many revolutions per minute must the wheel make so as to keep a speed of 66 km/hr ?
The area of a circle is 38.5 cm2. The circumference of the circle is
In Figure 2, two concentric circles with centre O, have radii 21 cm and 42 cm. If ∠AOB = 60°, find the area of the shaded region.

The speed of a car is 66km per hour. If each wheel of the car is 140cm in diameter, find the number if revolution made by each wheel per minute.
Diameters of different circles are given below. Find their circumference (Take π = `22/7`)
d = 70 cm
A wire of length 1320 cm is made into circular frames of radius 7 cm each. How many frames can be made?
Circumference of a circle is always ______.
The radii of the two circles are 19 cm and 9 cm respectively. The radius of the circle which has a circumference equal to the sum of the circumference of two circles is ____________.
