Advertisements
Advertisements
प्रश्न
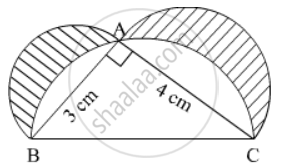
In the given figure, ∆ ABC is a right-angled triangle in which ∠ A is 90°. Semicircles are drawn on AB, AC and BC as diameters. Find the area of the shaded region
उत्तर
In right angled ΔABC
`AB^2 + AC^2 = BC^2`
`=> BC = sqrt(AB^2 + AC^2)= sqrt(3^2 + 4^2)`
`=> BC = sqrt(9 + 16) = sqrt25 = 5 cm`
Area of shaded region = {ar (ΔABC) + ar(semicircle on side AB) + ar(semicircle on side AC) } - ar(semicircle on side BC)
Area of shaded region = `[(1/2 xx 3 xx 4)+(1/2pi xx (3/2)^2) +(1/2pi xx (2)^2)] - (1/2pi xx (5/2)^2) cm^2`
`= 6 + 1/2pi(9/4 + 4 - 25/4) cm^2`
= 6 cm2
Hence, area of shaded region is 6 cm2
APPEARS IN
संबंधित प्रश्न
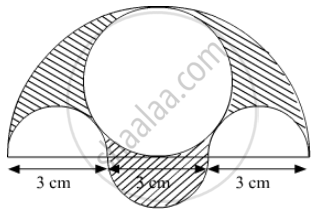
Three semicircles each of diameter 3 cm, a circle of diameter 4.5 cm and a semicircle of radius 4.5 cm are drawn in the given figure. Find the area of the shaded region
A gardener wants to fence a circular garden of diameter 21 m. Find the length of the rope he needs to purchase, if he makes 2 rounds of fence. Also find the costs of the rope, if it cost ₹ 4 per meter. (Take `pi = 22/7`)
Shazli took a wire of length 44 cm and bent it into the shape of a circle. Find the radius of that circle. Also find its area. If the same wire is bent into the shape of a square, what will be the length of each of its sides? Which figure encloses more area, the circle or the square? (Take `pi = 22/7`)
What is the perimeter of a square which circumscribes a circle of radius a cm?
The circumferences of two circles are in the ratio 2: 3. What is the ratio between their areas?
In the given figure, ABCD is a square of side 4 cm. A quadrant of a circle of radius 1 cm is drawn at each vertex of the square and a circle of diameter 2 cm is also drawn. Find the area of the shaded region. [π = 3.14]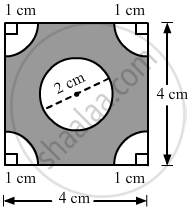
The circumference of a circle is equal to the sum of the circumference of two circles having diameters 36 cm and 20 cm. The radius of the new circle is
The sum of the radii of two circles is 10.5 cm and the difference of their circumferences is 13. 2 cm. Find the radii of the two circles.
The circumference of a circular field is 308 m. Find is:
(i) Radius
(ii) Area.
Find the area and perimeter of the circles with following: Radius = 2.8cm
