Advertisements
Advertisements
प्रश्न
In the given figure, ABCD is a square of side 4 cm. A quadrant of a circle of radius 1 cm is drawn at each vertex of the square and a circle of diameter 2 cm is also drawn. Find the area of the shaded region. [π = 3.14]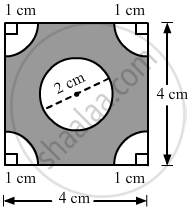
उत्तर
Area of the square ABCD =(Side)2
= 42
= 16 cm2
Area of the circle = πr2
Radius = 1 cm
Area = 3.14 × (1)2
= 3.14 cm2
Area of the quadrant of one circle`=1/4pi"r"^2`
`=1/4xx3.14xx1^2`
= 0.785 cm2
Area of the quadrants of four circles = 0.785 × 4 = 3.14 cm2
Area of the shaded region = Area of the square - Area of the circle - Area of the quadrants of four circles = 16-3.14-3.14 = 9.72 cm2
APPEARS IN
संबंधित प्रश्न
The wheel of a motor cycle is of radius 35 cm. How many revolutions per minute must the wheel make so as to keep a speed of 66 km/hr ?
Four equal circles, each of radius a units, touch each other. Show that the area between them is `(6/7"a"^2)` sq units.
The diameter of a wheel is 84 cm. How many revolutions will it make to cover 792 m?
Find the area and perimeter of the circle with the following :
Radius= 2.8 cm
Complete the table below.
| Radius (r) | Diameter (d) | Circumference (c) |
| 7 cm | ______ | _______ |
Complete the table below.
| Radius (r) | Diameter (d) | Circumference (c) |
| ...... | 28 cm | ...... |
Find the area and perimeter of the circles with following: Diameter = 35cm
Diameters of different circles are given below. Find their circumference (Take π = `22/7`)
d = 28 mm
A Rose garden is in the form of circle of radius 63 m. The gardener wants to fence it at the rate of ₹ 150 per metre. Find the cost of fencing?
The cost of fencing a circular race course at the rate of ₹ 8 per metre is ₹ 2112. Find the diameter of the race course
