Advertisements
Advertisements
प्रश्न
In the given figure, ∆ ABC is a right-angled triangle in which ∠ A is 90°. Semicircles are drawn on AB, AC and BC as diameters. Find the area of the shaded region
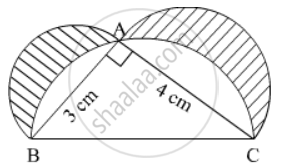
उत्तर
In right angled ΔABC
`AB^2 + AC^2 = BC^2`
`=> BC = sqrt(AB^2 + AC^2)= sqrt(3^2 + 4^2)`
`=> BC = sqrt(9 + 16) = sqrt25 = 5 cm`
Area of shaded region = {ar (ΔABC) + ar(semicircle on side AB) + ar(semicircle on side AC) } - ar(semicircle on side BC)
Area of shaded region = `[(1/2 xx 3 xx 4)+(1/2pi xx (3/2)^2) +(1/2pi xx (2)^2)] - (1/2pi xx (5/2)^2) cm^2`
`= 6 + 1/2pi(9/4 + 4 - 25/4) cm^2`
= 6 cm2
Hence, area of shaded region is 6 cm2
APPEARS IN
संबंधित प्रश्न
Find the circumference of a circle whose area is 301.84 cm2.
An arc of length 20𝜋 cm subtends an angle of 144° at centre of circle. Find the radius of the circle.
Find the angle subtended at the centre of circle of radius ‘a’ cm by an arc of length
`(api)/4` 𝑐𝑚
In circle of radius 6cm, chord of length 10 cm makes an angle of 110° at the centre of circle find Circumference of the circle
The outer circumference of a circular race track is 528m. The track is everywhere 14m
wide. Calculate the cost of leveling the track at rate of 50 paise per square metre.
The hypotenuse of a right-angled triangle is 65 cm and its base is 60 cm. Find the length of perpendicular and the area of the triangle.
The sum of the radii of two circles is 7 cm, and the difference of their circumferences is 8 cm. Find the circumference of the circles.
A cylindrical bucket, whose base radius is 20 cm, is filled with water to a height of 25 cm. A heavy iron spherical ball of radius 10 cm is dropped to submerge completely in water in the bucket. Find the increase in the level of water.
Find the area and perimeter of the circles with following: Diameter = 77cm
Find the area and perimeter of the following semicircles: Radius = 1.4cm
