Advertisements
Advertisements
प्रश्न
The hypotenuse of a right-angled triangle is 65 cm and its base is 60 cm. Find the length of perpendicular and the area of the triangle.
उत्तर
Hypotenuse = 65 cm
Base = 60 cm
In a right angled triangle,
`"(Hypotenuse)"^2="(Base)"^2+"(Perpendicular)"^2`
⇒`(65)^2=(60)^2+"(perpendicular)"^2`
⇒ `(65)^2-(60)^2+"(perpendicular)"^2`
⇒`"(Perpendicular)"^2=(65-60)(65+60)`
⇒`"(Perpendicular)"=5xx125`
⇒`"(Perpendicular)"^2=625`
⇒`"(Perpendicular)"^2=25 cm`
`"Area of triangle"=1/2xx"Base"xx"perpendicular"`
=`1/2xx60xx25`
=`750cm^2`
APPEARS IN
संबंधित प्रश्न
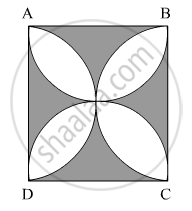
In Fig. 4, ABCD is a square of side 14 cm. Semi-circles are drawn with each side of square as diameter. Find the area of the shaded region.
(use `pi=22/7`)
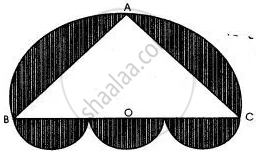
A doorway is decorated as shown in the figure. There are four semi-circles. BC, the diameter of the larger semi-circle is of length 84 cm. Centres of the three equal semicircles lie on BC. ABC is an isosceles triangle with AB = AC. If BO = OC, find the area of the shaded region. (Take `pi = 22/7`)
A copper wire when bent in the form of a square encloses an area of 484 cm2. The same wire is not bent in the form of a circle. Find the area enclosed by the circle.
The wheels of the locomotive of a train are 2.1 m in radius. They make 75 revolutions in one minute.
The radius of the circle is given below; find the area.
28 cm
The diameter of a wheel is 1.4m. How many revolutions does it make in moving a distance of 2.2 kms?
Each wheel of a car is of diameter 80 cm. How many completer revolutions does each wheel make in 10 minutes when the car is traveling at a speed of 66 km per hour?
The circumferences of two circles are in the ratio 5: 7, find the ratio between their radius.
The radius of a circular garden is 56 m. What would it cost to put a 4-round fence around this garden at a rate of 40 rupees per metre?
Circumferences of two circles are equal. Is it necessary that their areas be equal? Why?
