Advertisements
Advertisements
प्रश्न
A copper wire when bent in the form of a square encloses an area of 484 cm2. The same wire is not bent in the form of a circle. Find the area enclosed by the circle.
उत्तर
Area of the circle = 484 cm2
Area of the square = Side2
⇒ 484 = Side2
⇒ 222 = Side2
⇒ Side = 22 cm
Perimeter of the square = 4 × Side
Perimeter of the square = 4 × 22
= 88 cm
Length of the wire = 88 cm
Circumference of the circle = Length of the wire = 88 cm
Now, let the radius of the circle be r cm.
Thus, we have:
2πr = 88
`⇒ 2xx22/7xx"r"=88`
⇒ r = 14
Area of the circle = πr2
`=22/7xx14xx14`
= 616 cm2
Thus, the area enclosed by the circle is 616 cm2.
APPEARS IN
संबंधित प्रश्न
In the given figure, ABCD is a square of side 4 cm. A quadrant of a circle of radius 1 cm is drawn at each vertex of the square and a circle of diameter 2 cm is also drawn. Find the area of the shaded region. [π = 3.14]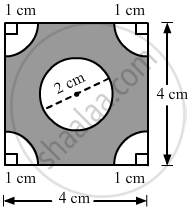
Find the area and perimeter of the circle with the following :
Radius= 10.5 cm
Find the area and perimeter of the circle with the following :
Diameter = 77 cm
Find the area and perimeter of the following semi-circle :
Radius= 1.4 cm
Find the area and perimeter of the following semi-circle :
Diameter= 5.6 cm
The cost of fencing a circular field at the rate of ₹ 240 per meter is ₹ 52,800. The field is to be ploughed at the rate of ₹ 12.50 per m2. Find the cost of pouching the field.
Each side of a square is 44 cm. Find its perimeter. If this perimeter is equal to the circumference of a circle, find the radius of the circle.
The area of a circle whose circumference is 22 cm, is ____________.
The distance around a circle is its ______.
