Advertisements
Advertisements
प्रश्न
A wire when bent in the form of an equilateral triangle encloses an area of `121sqrt(3) "cm"^2`. The same wire is bent to form a circle. Find the area enclosed by the circle.
उत्तर
Area of an equilateral triangle`=sqrt(3)/4xx("Side")^2`
`=> 121sqrt(3) = sqrt(3)/4xx("Side")^2`
`=> 121xx4 = ("Side")^2`
`=> "Side" = 22 "cm" `
Perimeter of an equilateral triangle = 3 × Side
= 3 × 22
= 66 cm
Length of the wire = 66 cm
Now, let the radius of the circle be r cm.
We know:
Circumference of the circle = Length of the wire
2π = 66
`=> 2 xx 22/7xx"r" = 66`
`=> "r" = (66xx7)/(2xx22)`
`=> "r" = 21/2`
⇒ r = 10.5
Thus, we have :
Area of the circle = πr2
`=22/7xx10.5xx10.5`
= 346.5 sq.cm
Area enclosed by the circle = 346.5 cm2
APPEARS IN
संबंधित प्रश्न
The minute hand of a clock is √21 𝑐𝑚 long. Find area described by the minute hand on the face of clock between 7 am and 7:05 am
The minute hand of clock is10cm long. Find the area of the face of the clock described by the minute hand between 8am and 8:25 am
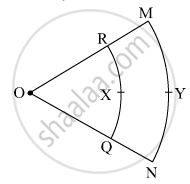
In the given figure, O is the centre of the sector. \[\angle\]ROQ = \[\angle\]MON = 60° . OR = 7 cm, and OM = 21 cm. Find the lengths of arc RXQ and arc MYN. (\[\pi = \frac{22}{7}\])
Three equal circles, each of radius 6 cm, touch one another as shown in the figure. Find the area of enclosed between them.

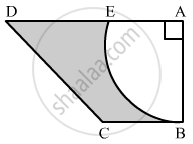
In the given figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region.
The circumference of a circle is equal to the sum of the circumference of two circles having diameters 36 cm and 20 cm. The radius of the new circle is
If the perimeter of a square is equal to the circumference of a circle then the ratio of their areas is
The diameter of a wheel is 1.4m. How many revolutions does it make in moving a distance of 2.2 kms?
Find the volume and the surface area of the spheres in the following :
Diameter= 6.3 cm
A circular racing track has inner circumference 528 m and outer circumference 616 m. Find the width of the track.
