Advertisements
Advertisements
Question
A wire when bent in the form of an equilateral triangle encloses an area of `121sqrt(3) "cm"^2`. The same wire is bent to form a circle. Find the area enclosed by the circle.
Solution
Area of an equilateral triangle`=sqrt(3)/4xx("Side")^2`
`=> 121sqrt(3) = sqrt(3)/4xx("Side")^2`
`=> 121xx4 = ("Side")^2`
`=> "Side" = 22 "cm" `
Perimeter of an equilateral triangle = 3 × Side
= 3 × 22
= 66 cm
Length of the wire = 66 cm
Now, let the radius of the circle be r cm.
We know:
Circumference of the circle = Length of the wire
2π = 66
`=> 2 xx 22/7xx"r" = 66`
`=> "r" = (66xx7)/(2xx22)`
`=> "r" = 21/2`
⇒ r = 10.5
Thus, we have :
Area of the circle = πr2
`=22/7xx10.5xx10.5`
= 346.5 sq.cm
Area enclosed by the circle = 346.5 cm2
APPEARS IN
RELATED QUESTIONS
Below fig shows a sector of a circle, centre O. containing an angle 𝜃°. Prove that
Area of shaded region is`r^2/2(tantheta −(pitheta)/180)`
Choose the correct alternative answer for the following question.
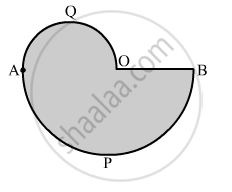
In the given figure, APB and AQO are semicircles and AO = OB. If the perimeter of the figure is 40 cm, find the area of the shaded region.
A wire bent in the form of an equilateral triangle has an area of 121 `sqrt 3` cm2. If the same wire is bent into the form of a circle , find the area enclosed by the wire.
The circumference of a circular field is 308 m. Find is:
(i) Radius
(ii) Area.
Each wheel of a car is of diameter 80 cm. How many completer revolutions does each wheel make in 10 minutes when the car is traveling at a speed of 66 km per hour?
Find the dimensions of a rectangular park whose perimeter is 60 m and area 200 m2.
The radius of two circles are in the ratio 3 : 5, find the ratio between their circumferences.
Construct the circumcircle of the ABC when BC = 6 cm, B = 55° and C = 70°.
Find the radius of a circle whose circumference is equal to the sum of the circumferences of two circles of radii 15 cm and 18 cm.
