Advertisements
Advertisements
Question
A wire bent in the form of an equilateral triangle has an area of 121 `sqrt 3` cm2. If the same wire is bent into the form of a circle , find the area enclosed by the wire.
Solution
Area of equi I ater al triangle = 121 `sqrt 3` cm2
`=> ("s"^2 sqrt 3)/4 = 121 sqrt 3`
`=> "s"^2 - 484`
`=> "s" = 22 "cm"`
Side of the triangle = 22 cm
Perimeter of the triangle= 3 x 22 = 66 cm
Perimeter of the circle = perimeter of the triangle
`=> 2 pi "r" = 66`
`=> "r" = 66 xx 7/22 xx 1/2`
⇒ r = 10.5 cm
Radius of circle = 10.5 cm
Area of cirde = π r2
`= 22/7 xx 10.5 xx 10.5`
= 346.5 cm2
Hence, area of the circle = 346.5 cm2
APPEARS IN
RELATED QUESTIONS
The circumference of a circle exceeds the diameter by 16.8 cm. Find the radius of the circle.
A wire is looped in the form of a circle of radius 28 cm. It is re-bent into a square form. Determine the length of the side of the square.
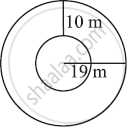
Find the circumference of the inner and the outer circles, shown in the adjoining figure? (Take π = 3.14)
The circumference of a circle exceeds diameter by 16.8 cm. Find the circumference of
circle.
Find the circumferences of a circle whose radius is 7 cm.
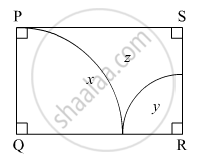
In the given figure,
\[\square\] PQRS is a rectangle. If PQ = 14 cm, QR = 21 cm, find the areas of the parts x, y, and z.
The difference between the circumference and radius of a circle is 37cm. Using `pi = 22/7` , find the circumference of the circle.
A square ABCD is inscribed in a circle of radius r. Find the area of the square.
The side of a square is 10 cm. Find the area of the inscribed circle [π = 3.14]
The area of a square is the same as the area of a square. Their perimeters are in the ratio
A wire when bent in the form of a square encloses an area of 484 cm2. If the same wire is bent into the form of a circle, find the area of the circle.
Find the volume and the surface area of the spheres in the following :
Radius= 2.1 cm
The diameters of the front and the rear wheels of a tractor are 63 cm and 1.54 m respectively. The rear wheel is rotating at `24 6/11` revolutions per minute. Find:
(i) the revolutions per minute made by the front wheel.
(ii) the distance traveled bu the tractor in 40 minutes.
Complete the table below.
| Radius (r) | Diameter (d) | Circumference (c) |
| ...... | ...... | 616 cm |
Find the area and perimeter of the circles with following: Radius = 2.8cm
The diameter of a wheel is 1.4m. How many revolutions does make in moving a distance of 2.2km?
The circumference of a circle exceeds its diameter by 450 cm. Find the area of the circle.
The numerical value of the area of a circle is greater than the numerical value of its circumference. Is this statement true? Why?
Circumference ‘C’ of a circle can be found by multiplying diameter ‘d’ with ______.
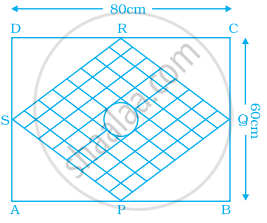
ABCD is a given rectangle with length as 80 cm and breadth as 60 cm. P, Q, R, S are the midpoints of sides AB, BC, CD, DA respectively. A circular rangoli of radius 10 cm is drawn at the centre as shown in the given figure. Find the area of shaded portion.