Advertisements
Advertisements
Question
The diameters of the front and the rear wheels of a tractor are 63 cm and 1.54 m respectively. The rear wheel is rotating at `24 6/11` revolutions per minute. Find:
(i) the revolutions per minute made by the front wheel.
(ii) the distance traveled bu the tractor in 40 minutes.
Solution
Given the diameter of the front and rear wheels are 63 cm = 0.63 m and 1.54 m respectively,
The radius of the rear wheel = `1.54/2` = 0.77 m.
and radius of the front wheel = `0.63/2` = 0.315 m
Distance traveled by tractor in one revolution of the rear wheel = circumference of the rear wheel
= 2πr
= 2 x `22/7` x 0.77
= 4.84 m
The rear wheel rotates at `24 6/11` revolutions per minute
= `270/11` revolutions per minute
Since in one revolution, the distance traveled by the rear wheel = 4.84 m
So, in `270/11` revolutions, the tractor travels `270/11` x 4.84 = 118.8 m
Let the number of revolutions made by the front wheel be x.
(i) Now, the number of revolutions made by the front wheel in one minute x circumference of the wheel
= the distance traveled by tractor in one minute
⇒ `x xx 2 xx 22/7 xx 0.315 = 118.8`
⇒ `xx = [ 118.8 xx 7 ]/[ 2 xx 22 xx 0.315 ]` = 60
(ii) Distance traveled by tractor in 40 minutes
= number of revolutions made by the rear wheel in 40 minutes
x circumferent of the rear wheel
= `270/11 xx 40 xx 4.84 = 4752` m
APPEARS IN
RELATED QUESTIONS
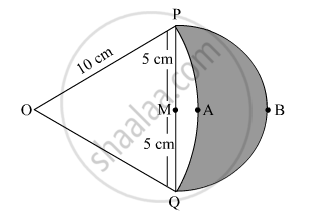
In Fig. 7, are shown two arcs PAQ and PBQ. Arc PAQ is a part of circle with centre O and radius OP while arc PBQ is a semi-circle drawn on PQ ad diameter with centre M. If OP = PQ = 10 cm show that area of shaded region is `25(sqrt3-pi/6)cm^2`.
The inner circumference of a circular track is 220 m. The track is 7m wide everywhere. Calculate the cost of putting up a fence along the outer circle at the rate of j – 2 per metre. (Use π = 22/7)
The area of rhombus is `480cm^2` , and one of its diagonal measures 48 cm. Find
(i) the length of the other diagonal,
(ii) the length of each of the sides
(iii) its perimeter
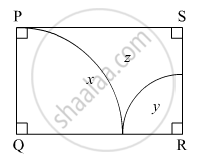
In the given figure,
\[\square\] PQRS is a rectangle. If PQ = 14 cm, QR = 21 cm, find the areas of the parts x, y, and z.
The circumferences of two circles are in the ratio 3 : 4. The ratio of their areas is
In a circle of radius 14 cm, an arc subtends an angle of 120° at the centre. If `sqrt(3) = 1.73` then the area of the segment of the circle is
Find the area and perimeter of the circle with the following:
Diameter= 35 cm
Find the total surface area and volume of a hemisphere whose radius is 10 cm.
A metal wire, when bent in the form of an equilateral triangle of largest area, encloses an area of 484 `sqrt3` cm2. If the same wire is bent into the form of a circle of largest area, find the area of this circle.
Find the area and perimeter of the circles with following: Diameter = 35cm
